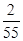题目内容
设E,F是正方体AC1的棱AB和D1C1的中点,在正方体的12条面对角线中,与截面A1ECF成60°角的对角线的数目是( )
| A.0 | B.2 | C.4 | D.6 |
C
分析:先把六个面分为三组,在一组组的进行研究,找到直线与截面法向量的夹角即可得到结论.
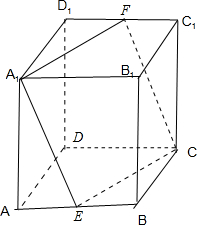
解:首先,把六个面分成三组,AA1D1D和BB1C1C对截面的关系是一样的,其他四个是一样的,
以点D为原点,AD所在直线为X轴,DC所在直线为Y轴,DD1所在直线为Z轴,
设正方体棱长为2;
则A(2,0,0),D(0,0,0),B(2,2,0),C(0,2,0),E(2,1,0),
F(0,1,2),A1(2,0,2),B1(2,2,2,),C1(0,2,2),D1(0,0,2);
∴
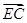 =(-2,1,0),
=(-2,1,0),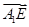 =((0,1,2),
=((0,1,2),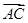 =(-2,2,0),
=(-2,2,0),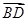 =(-2,-2,0),
=(-2,-2,0),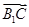 =(-2,0,-2),
=(-2,0,-2),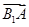 =(0,-2,-2);
=(0,-2,-2);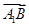 =(0,2,-2)
=(0,2,-2)因为要想面对角线截面A1ECF成60°角,需要直线与法向量的夹角为30度,即其余弦值为±
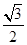 .
.设截面A1ECF的法向量为
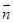 =(x,y,z),
=(x,y,z),由
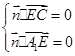 ?
?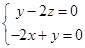 ?
?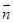 =(1,2,1),且|
=(1,2,1),且|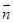 |=
|=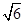 ,
,因为cos<
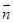 ,
,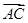 >=
>=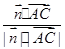 =
=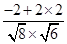 =
=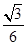 ≠±
≠±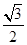 ;
;cos<
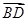 ,
,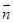 >=
>=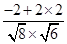 =-
=-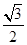 ,
,cos<
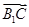 ,
,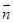 >=
>=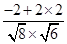 ≠±
≠±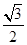 ;
;cos(
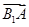 ,
,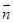 >=
>=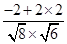 =-
=-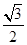 ;
;cos<
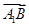 ,
,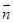 >=
>=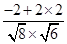 ≠±
≠±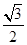 ;
;再看AA1D1D这个面里,
AD1与EF平行,不是,
所以,一共四条.
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
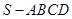 中,
中, 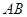 ∥
∥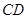 ,
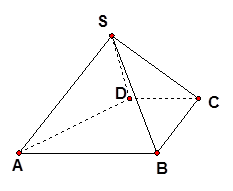
,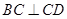 ,侧面
,侧面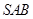 为等边三角形.
为等边三角形.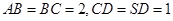 .
. 
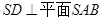
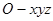 中,点
中,点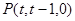 与点
与点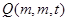 距离的最小值为 .
距离的最小值为 . 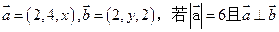 ,求
,求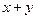 的值.
的值. 且
且 则x-y=
则x-y= 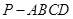 中,底面
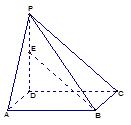
中,底面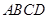 是正方形,
是正方形,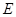 为
为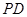 中点,若
中点,若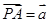 ,
,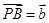 ,
,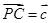 ,则
,则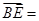 ( *** )
( *** )
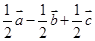
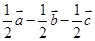
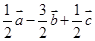
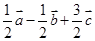
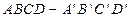 的棱长为a,M为
的棱长为a,M为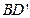 的中点,点N在
的中点,点N在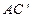 上,且
上,且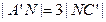 ,试求MN的长.
,试求MN的长.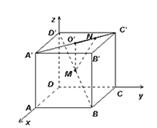
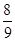 ,则λ的值为
,则λ的值为