题目内容
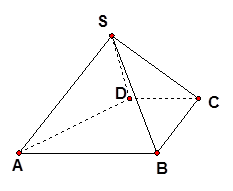
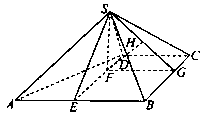
如图,四棱锥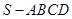 中,
中, 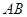 ∥
∥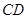 ,
,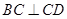 ,侧面
,侧面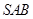 为等边三角形.
为等边三角形.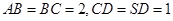 .
.
(1)证明: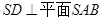
(2)求AB与平面SBC所成角的大小。
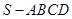 中,
中, 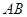 ∥
∥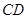 ,
,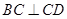 ,侧面
,侧面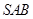 为等边三角形.
为等边三角形.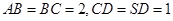 .
. 
(1)证明:
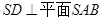
(2)求AB与平面SBC所成角的大小。
(1)见解析 (2)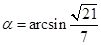
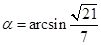
(1)取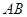 中点
中点 ,连结
,连结 ,则四边形
,则四边形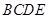 为矩形,
为矩形,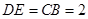 ,连结
,连结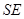 ,则
,则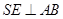 ,
,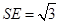 .
.
又 ,故
,故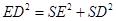 ,
,
所以 为直角. 3分
为直角. 3分
由 ,
, ,
, ,得
,得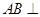 平面
平面 ,所以
,所以 .
.
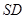 与两条相交直线
与两条相交直线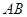 、
、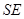 都垂直.
都垂直.
所以 平面
平面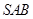 . 6分
. 6分
另解:由已知易求得 ,于是
,于是 .可知
.可知 ,同理可得
,同理可得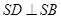 ,又
,又 .所以
.所以 平面
平面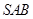 . 6分
. 6分
(2)由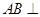 平面
平面 知,平面
知,平面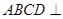 平面
平面 .
.
作 ,垂足为
,垂足为 ,则
,则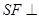 平面ABCD,
平面ABCD,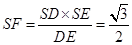 .
.
作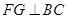 ,垂足为
,垂足为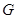 ,则
,则 .
.
连结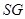 .则
.则 .
.
又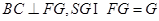 ,故
,故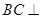 平面
平面 ,平面
,平面 平面
平面 . 9分
. 9分
作 ,
, 为垂足,则
为垂足,则 平面
平面 .
.
 ,即
,即 到平面
到平面 的距离为
的距离为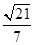 .
.
由于 ,所以
,所以 平面
平面 ,
,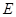 到平面
到平面 的距离
的距离 也为
也为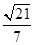 .
.
设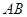 与平面
与平面 所成的角为
所成的角为 ,则
,则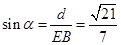 ,
,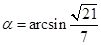 . 12分
. 12分
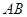 中点
中点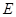 ,连结
,连结 ,则四边形
,则四边形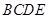 为矩形,
为矩形,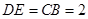 ,连结
,连结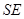 ,则
,则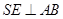 ,
,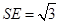 .
.
又
 ,故
,故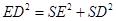 ,
,所以
 为直角. 3分
为直角. 3分由
 ,
, ,
, ,得
,得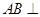 平面
平面 ,所以
,所以 .
.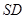 与两条相交直线
与两条相交直线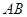 、
、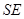 都垂直.
都垂直.所以
 平面
平面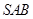 . 6分
. 6分另解:由已知易求得
 ,于是
,于是 .可知
.可知 ,同理可得
,同理可得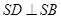 ,又
,又 .所以
.所以 平面
平面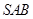 . 6分
. 6分(2)由
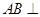 平面
平面 知,平面
知,平面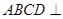 平面
平面 .
.作
 ,垂足为
,垂足为 ,则
,则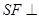 平面ABCD,
平面ABCD,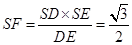 .
.作
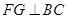 ,垂足为
,垂足为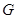 ,则
,则 .
.连结
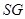 .则
.则 .
.又
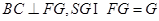 ,故
,故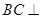 平面
平面 ,平面
,平面 平面
平面 . 9分
. 9分作
 ,
, 为垂足,则
为垂足,则 平面
平面 .
. ,即
,即 到平面
到平面 的距离为
的距离为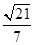 .
.由于
 ,所以
,所以 平面
平面 ,
,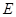 到平面
到平面 的距离
的距离 也为
也为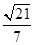 .
.设
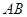 与平面
与平面 所成的角为
所成的角为 ,则
,则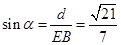 ,
,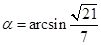 . 12分
. 12分
练习册系列答案
相关题目
 ,使
,使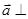
 成立的x与使
成立的x与使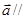
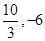
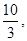 6
6 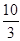
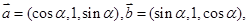 则向量
则向量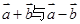 的夹角是_________.
的夹角是_________. 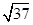
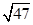
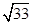
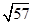
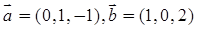 ,若向量
,若向量 与向量
与向量 互相垂直,则
互相垂直,则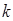 的值是 ( )
的值是 ( )
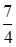

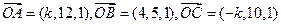 ,且A、B、C三点共线,
,且A、B、C三点共线,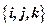 为单位正交基,且
为单位正交基,且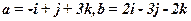 ,则向量
,则向量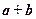 的坐标是______________________.
的坐标是______________________.