Question

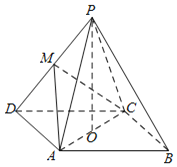
【题目】如图，已知四边形ABCD由Rt△ABC和Rt△BCD拼接而成，其中∠BAC＝∠BCD＝90°，∠DBC＝30°，AB＝AC，，将△ABC沿着BC折起，

（1）若，求异面直线AB和CD所成角的余弦值；

（2）当四面体ABCD的体积最大时，求二面角A﹣BC﹣D的余弦值.

Answer 1

【答案】（1）（2）

【解析】

（1）根据异面直角所成角的空间向量计算公式，再利用题给信息构造空间直角坐标系，即可求出所求角；

（2）当平面ABC⊥平面BCD时，四面体ABCD体积有最大值，即可得答案.

（1）因为∠BAC＝90°，且AB＝AC，BC，

∴，∴AB＝AC＝AD，

∴作AO⊥平面BCD，垂足O必为△BCD的外心，

又因为△BCD中，∠BCD＝90°，△BCD的外心在斜边中点处，即O点为BD中点，

则以OA方向建立z轴，过O点作x轴平行于BC，作y轴平行于CD，如图所示

得坐标，，，

∴

∴（0，﹣2，0），，

设AB与CD所成角为，

则；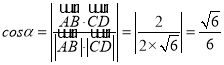

（2）当平面ABC⊥平面BCD时，四面体ABCD体积有最大值，此时二面角A﹣BC﹣D为90°，其余弦值为0.