题目内容
【题目】已知抛物线y=﹣ ![]() +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).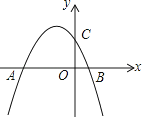
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
【答案】
(1)
解:抛物线的解析式为y=﹣ ![]() (x+4)(x﹣1),即y=﹣
(x+4)(x﹣1),即y=﹣ ![]() x2﹣
x2﹣ ![]() x+2;
x+2;
(2)
解:存在.
当x=0,y═﹣ ![]() x2﹣
x2﹣ ![]() x+2=2,则C(0,2),
x+2=2,则C(0,2),
∴OC=2,
∵A(﹣4,0),B(1,0),
∴OA=4,OB=1,AB=5,
当∠PCB=90°时,
∵AC2=42+22=20,BC2=22+12=5,AB2=52=25
∴AC2+BC2=AB2
∴△ACB是直角三角形,∠ACB=90°,
∴当点P与点A重合时,△PBC是以BC为直角边的直角三角形,此时P点坐标为(﹣4,0);
当∠PBC=90°时,PB∥AC,如图1,
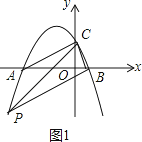
设直线AC的解析式为y=mx+n,
把A(﹣4,0),C(0,2)代入得 ![]() ,解得
,解得  ,
,
∴直线AC的解析式为y= ![]() x+2,
x+2,
∵BP∥AC,
∴直线BP的解析式为y= ![]() x+p,
x+p,
把B(1,0)代入得 ![]() +p=0,解得p=﹣
+p=0,解得p=﹣ ![]() ,
,
∴直线BP的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
解方程组 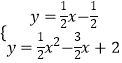 得
得 ![]() 或
或 ![]() ,此时P点坐标为(﹣5,﹣3);
,此时P点坐标为(﹣5,﹣3);
综上所述,满足条件的P点坐标为(﹣4,0),P2(﹣5,﹣3);
(3)
解:存在点E,设点E坐标为(m,0),F(n,﹣ ![]() n2﹣
n2﹣ ![]() n+2)
n+2)
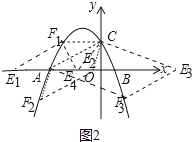
①当AC为边,CF1∥AE1,易知CF1=3,此时E1坐标(﹣7,0),
②当AC为边时,AC∥EF,易知点F纵坐标为﹣2,
∴﹣ ![]() n2﹣
n2﹣ ![]() n+2=﹣2,解得n=
n+2=﹣2,解得n= ![]() ,得到F2(
,得到F2( ![]() ,﹣2),F3(
,﹣2),F3( ![]() ,﹣2),
,﹣2),
根据中点坐标公式得到: ![]() =
= ![]() 或
或 ![]() =
= ![]() ,
,
解得m= ![]() 或
或 ![]() ,
,
此时E2( ![]() ,0),E3(
,0),E3( ![]() ,0),
,0),
③当AC为对角线时,AE4=CF1=3,此时E4(﹣1,0),
综上所述满足条件的点E为(﹣7,0)或(﹣1,0)或( ![]() ,﹣2)或(
,﹣2)或( ![]() ,﹣2).
,﹣2).
【解析】本题考查二次函数综合题、一次函数、勾股定理、平行四边形的判定和性质、中点坐标公式等知识,解题的关键是构建一次函数利用方程组解决点P坐标,学会分类讨论,学会用方程的思想解决问题,属于中考压轴题.
(1)因为抛物线经过点A(﹣4,0),B(1,0),所以可以设抛物线为y=﹣ ![]() (x+4)(x﹣1),展开即可解决问题;
(x+4)(x﹣1),展开即可解决问题;
(2)先证明∠ACB=90°,点A就是所求的点P,求出直线AC解析式,再求出过点B平行AC的直线的解析式,利用方程组即可解决问题;
(3)分AC为平行四边形的边,AC为平行四边形的对角线两种切线讨论即可解决问题.