题目内容
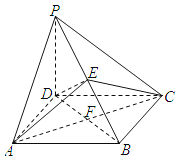
【题目】已知M是正四面体ABCD棱AB的中点,N是棱CD上异于端点C,D的任一点,则下列结论中,正确的个数有( )
(1)MN⊥AB;
(2)若N为中点,则MN与AD所成角为60°;
(3)平面CDM⊥平面ABN;
(4)不存在点N,使得过MN的平面与AC垂直.
A.1
B.2
C.3
D.4
【答案】C
【解析】解:(1)连结MC,MD,由三角形三线合一可得AB⊥CM,AB⊥DM,∴AB⊥平面MCD,
∵MN平面MCD,∴AB⊥MN,故(1)正确;
(2)取BD中点E,连结ME,NE,则∠NME为MN与AD所成角,
连结BN,由(1)知BM⊥MN,设正四面体棱长为1,则BM=![]() , BN=
, BN=![]() , ∴MN=
, ∴MN=![]() ,
,
ME=NE=![]() , ∴cos∠NME=
, ∴cos∠NME=![]() =
=![]() , ∴∠NME=45°,故(2)不正确;
, ∴∠NME=45°,故(2)不正确;
(3)由(1)知AB⊥平面CDM,∵AB平面ABN,∴平面CDM⊥平面ABN,故(3)正确;
(4)取BC早点F,连结MF,DF,假设存在点N,使得过MN的平面与AC垂直,
∴AC⊥MN,∵MF∥AC,∴MF⊥MN,
∵DF=DM=![]() , ∴∠FMD<90°,同理,∠CMF<90°.
, ∴∠FMD<90°,同理,∠CMF<90°.
当N从D向C移动时,∠FMN先减小,后增大,故∠FMN<90°,与MF⊥MN矛盾.
∴不存在点N,使得过MN的平面与AC垂直,故(4)正确.
故选:C.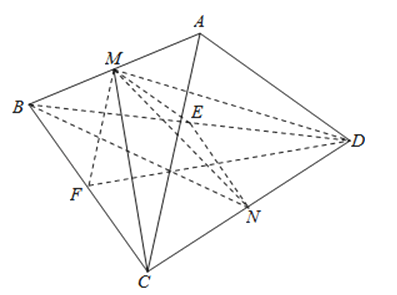
【考点精析】关于本题考查的平面与平面垂直的判定,需要了解一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】“累积净化量![]() ”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据
”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据![]() 《空气净化器》国家标准,对空气净化器的累计净化量
《空气净化器》国家标准,对空气净化器的累计净化量![]() 有如下等级划分:
有如下等级划分:
累积净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器(共5000台)的质量,随机抽取![]() 台机器作为样本进行估计,已知这
台机器作为样本进行估计,已知这![]() 台机器的累积净化量都分布在区间
台机器的累积净化量都分布在区间![]() 中,按照
中,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均匀分组,其中累积净化量在
均匀分组,其中累积净化量在![]() 的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
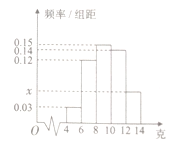
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共5000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累积净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.