题目内容
【题目】数列{an}满足:2a1+22a2+23a3+…+2nan=(n+1)2(n∈N*),则数列{an}的前n项和为 Sn= .
【答案】![]() ﹣
﹣ ![]()
【解析】解:∵2a1+22a2+23a3+…+2nan=(n+1)2(n∈N*), ∴2a1=22 , 解得a1=2.
n≥2时,2a1+22a2+23a3+…+2n﹣1an﹣1=n2 , 可得:2nan=2n+1,
∴an= ![]() .
.
∴an= 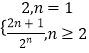 .
.
则n=1时,S1=2.
n≥2时,数列{an}的前n项和Sn=2+ ![]() +
+ ![]() …+
…+ ![]() .
.![]() =1+
=1+ ![]() +…+
+…+ ![]() +
+ ![]() ,
,
∴ ![]() =1+
=1+ ![]() +2
+2 ![]() ﹣
﹣ ![]() =2
=2 ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴Sn= ![]() ﹣
﹣ ![]() .(n=1时也成立).
.(n=1时也成立).
所以答案是: ![]() ﹣
﹣ ![]() .
.
【考点精析】利用数列的前n项和对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系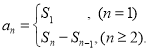 .
.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目