题目内容
3.已知a>0,b>0,a+4b=ab,则a+b的最小值是9.分析 由题意可得$\frac{1}{b}$+$\frac{4}{a}$=1,可得a+b=(a+b)($\frac{1}{b}$+$\frac{4}{a}$)=5+$\frac{a}{b}$+$\frac{4b}{a}$,由基本不等式求最值可得.
解答 解:∵a>0,b>0,a+4b=ab,
∴$\frac{a+4b}{ab}$=1,即$\frac{1}{b}$+$\frac{4}{a}$=1,
∴a+b=(a+b)($\frac{1}{b}$+$\frac{4}{a}$)
=5+$\frac{a}{b}$+$\frac{4b}{a}$≥5+2$\sqrt{\frac{a}{b}•\frac{4b}{a}}$=9
当且仅当$\frac{a}{b}$=$\frac{4b}{a}$即a=6且b=3时取等号,
故答案为:9
点评 本题考查基本不等式求最值,适当变形是解决问题的关键,属基础题.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
13.已知函数f(x)=sin(2x+φ)(|φ|<$\frac{π}{2}$),且f($\frac{π}{12}$)=1,为了得到g(x)=sin2x的图象,则只要将f(x)的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
15.设α、β是两个不同的平面,l、m为两条不同的直线,命题p:若α∥β,l?α,m?β,则l∥m,命题q:l∥α,m⊥l,m?β,则α⊥β则下列命题为真命题的是( )
| A. | p∨q | B. | p∧q | C. | (¬p)∨q | D. | p∧(¬q) |
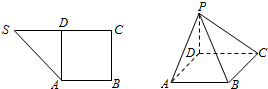 如图1,在直角梯形SABC中,∠B=∠C=$\frac{π}{2}$,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.
如图1,在直角梯形SABC中,∠B=∠C=$\frac{π}{2}$,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.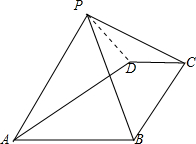 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=$\frac{π}{2}$,AD=2$\sqrt{2}$,AB=3DC=3.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=$\frac{π}{2}$,AD=2$\sqrt{2}$,AB=3DC=3.