题目内容
7.已知函数f(x)=sin(ωx+$\frac{π}{12}$)的图象经过点P(-$\frac{π}{12}$,0),图象上与点P最近的一个最高点是Q($\frac{5π}{12}$,1).(1)求ω的值;
(2)若cosθ=$\frac{4}{5}$,θ∈(0,$\frac{π}{2}$),求f(2θ-$\frac{π}{3}$).
分析 (1)由条件利用正弦函数的周期性求得φ的值.
(2)由(1)可知函数f(x)=sin(x+$\frac{π}{12}$),可得f(2θ-$\frac{π}{3}$)=$\frac{\sqrt{2}}{2}$(sin2θ-cos2θ).利用同角三角函数的基本关系,二倍角公式求得sin2θ 和cos2θ 的值,可得f(2θ-$\frac{π}{3}$)的值.
解答 解:(1)由题意可得$\frac{1}{4}$T=$\frac{π}{2ω}$=$\frac{5π}{12}$+$\frac{π}{12}$=$\frac{π}{2}$,求得ω=1.
(2)由(1)可知函数f(x)=sin(x+$\frac{π}{12}$),故f(2θ-$\frac{π}{3}$)=sin(2θ-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$(sin2θ-cos2θ).
再根据cosθ=$\frac{4}{5}$,θ∈(0,$\frac{π}{2}$),可得sinθ=$\frac{3}{5}$,sin2θ=2sinθcosθ=$\frac{24}{25}$,cos2θ=2cos2θ-1=$\frac{7}{25}$,
∴f(2θ-$\frac{π}{3}$)=sin(2θ-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$(sin2θ-cos2θ)=$\frac{\sqrt{2}}{2}$($\frac{24}{25}$-$\frac{7}{25}$)=$\frac{17\sqrt{2}}{50}$.
点评 本题主要考查正弦函数的周期性,同角三角函数的基本关系,二倍角公式,属于基础题.

练习册系列答案
相关题目
17.若直线ax-y+1=0与直线2x+y+2=0平行,则a的值为( )
| A. | -2 | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
15.设α、β是两个不同的平面,l、m为两条不同的直线,命题p:若α∥β,l?α,m?β,则l∥m,命题q:l∥α,m⊥l,m?β,则α⊥β则下列命题为真命题的是( )
| A. | p∨q | B. | p∧q | C. | (¬p)∨q | D. | p∧(¬q) |
2.已知A(1,2,1),B(-1,3,4),C(1,1,1),$\overrightarrow{AP}$=2$\overrightarrow{PB}$,则$\overrightarrow{PC}$=( )
| A. | (-$\frac{1}{3}$,$\frac{8}{3}$,3) | B. | ($\frac{1}{3}$,-$\frac{8}{3}$,-3) | C. | (-$\frac{4}{3}$,$\frac{5}{3}$,2) | D. | ($\frac{4}{3}$,-$\frac{5}{3}$,-2) |
19.过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是( )
| A. | 4x-3y-19=0 | B. | 4x+3y-13=0 | C. | 3x-4y-16=0 | D. | 3x+4y-8=0 |
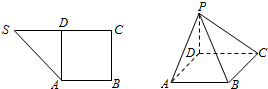 如图1,在直角梯形SABC中,∠B=∠C=$\frac{π}{2}$,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.
如图1,在直角梯形SABC中,∠B=∠C=$\frac{π}{2}$,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.