题目内容
如图①所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4.如图②所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连结AB,设点F是AB的中点.
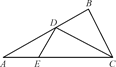 图①
图①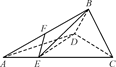 图②
图②
(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥B-DEG的体积.
 图①
图① 图②
图②(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥B-DEG的体积.
(1)见解析(2)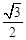
(1)证明:在题图①中,
∵AC=6,BC=3,∠ABC=90°,∴∠ACB=60°.
∵CD为∠ACB的平分线,
∴∠BCD=∠ACD=30°.∴CD=2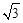 .
.
∵CE=4,∠DCE=30°,∴DE=2.
则CD2+DE2=EC2.∴∠CDE=90°.DE⊥DC.
在题图②中,∵平面BCD⊥平面ACD,平面BCD∩平面ACD=CD,DE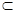 平面ACD,∴DE⊥平面BCD.
平面ACD,∴DE⊥平面BCD.
(2)解:在题图②中,∵EF∥平面BDG,EF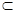 平面ABC,平面ABC∩平面BDG=BG,∴EF∥BG.
平面ABC,平面ABC∩平面BDG=BG,∴EF∥BG.
∵点E在线段AC上,CE=4,点F是AB的中点,
∴AE=EG=CG=2.
作BH⊥CD交于H.∵平面BCD⊥平面ACD,
∴BH⊥平面ACD.由条件得BH=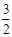 .S△DEG=
.S△DEG=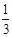 S△ACD=
S△ACD=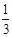 ×
×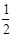 AC·CD·sin30°=
AC·CD·sin30°=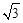 .
.
三棱锥B-DEG的体积V=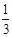 S△DEG·BH=
S△DEG·BH=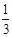 ×
×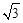 ×
×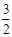 =
=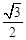
∵AC=6,BC=3,∠ABC=90°,∴∠ACB=60°.
∵CD为∠ACB的平分线,
∴∠BCD=∠ACD=30°.∴CD=2
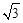 .
.∵CE=4,∠DCE=30°,∴DE=2.
则CD2+DE2=EC2.∴∠CDE=90°.DE⊥DC.
在题图②中,∵平面BCD⊥平面ACD,平面BCD∩平面ACD=CD,DE
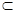 平面ACD,∴DE⊥平面BCD.
平面ACD,∴DE⊥平面BCD.
(2)解:在题图②中,∵EF∥平面BDG,EF
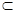 平面ABC,平面ABC∩平面BDG=BG,∴EF∥BG.
平面ABC,平面ABC∩平面BDG=BG,∴EF∥BG.∵点E在线段AC上,CE=4,点F是AB的中点,
∴AE=EG=CG=2.
作BH⊥CD交于H.∵平面BCD⊥平面ACD,
∴BH⊥平面ACD.由条件得BH=
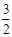 .S△DEG=
.S△DEG=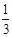 S△ACD=
S△ACD=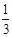 ×
×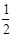 AC·CD·sin30°=
AC·CD·sin30°=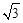 .
.三棱锥B-DEG的体积V=
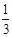 S△DEG·BH=
S△DEG·BH=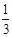 ×
×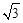 ×
×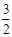 =
=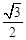

练习册系列答案
相关题目
 中,侧棱
中,侧棱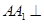 底面
底面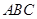 ,
, 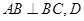 为
为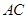 的中点,
的中点,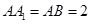 .
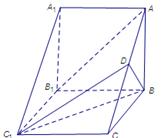
.
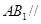 平面
平面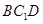 ;
;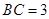 ,求三棱锥
,求三棱锥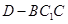 的体积.
的体积. 平面ABC.
平面ABC.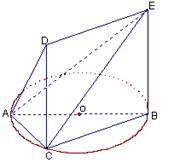
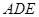 ;
;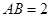 ,
,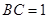 ,
,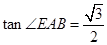 ,试求该简单组合体的体积V.
,试求该简单组合体的体积V. ABCD中,PA⊥底面ABCD,PA=2
ABCD中,PA⊥底面ABCD,PA=2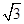 ,BC="CD=2," ∠ACB=∠ACD=
,BC="CD=2," ∠ACB=∠ACD=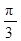 .
.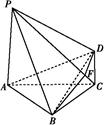
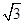 ,则正三棱锥SABC外接球的表面积是________.
,则正三棱锥SABC外接球的表面积是________.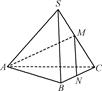
 中,
中, 、
、 分别是棱
分别是棱 、
、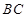 的中点,且
的中点,且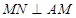 ,若侧棱
,若侧棱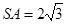 ,则正三棱锥
,则正三棱锥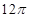
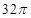
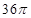
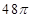
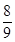
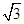
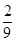
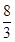
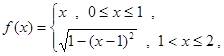 将
将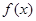 的图像与
的图像与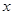 轴围成的封闭图形绕
轴围成的封闭图形绕