题目内容
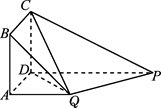
如图,一简单组合体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC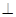 平面ABC.
平面ABC.
(1)证明:平面ACD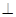 平面
平面 ;
;
(2)若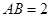 ,
,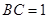 ,
,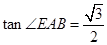 ,试求该简单组合体的体积V.
,试求该简单组合体的体积V.
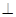 平面ABC.
平面ABC.
(1)证明:平面ACD
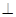 平面
平面 ;
;(2)若
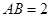 ,
,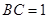 ,
,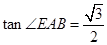 ,试求该简单组合体的体积V.
,试求该简单组合体的体积V.(1)详见解析;(2)该简单几何体的体积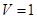 .
.
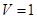 .
.试题分析:(1)欲证平面
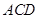 ⊥平面
⊥平面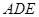 ,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,本题根据面面垂直的判定定理可知在平面
,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,本题根据面面垂直的判定定理可知在平面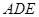 内找一条直线与平面
内找一条直线与平面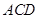 垂直,而由已知
垂直,而由已知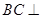 平面
平面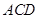 ,
,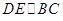 ,可得
,可得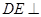 平面
平面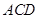 ,从而可得平面
,从而可得平面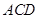 ⊥平面
⊥平面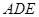 ;(2)所求简单组合体的体积进行分解:
;(2)所求简单组合体的体积进行分解: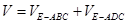 ,然后利用体积公式进行求解,关键是几何体的高的求解.
,然后利用体积公式进行求解,关键是几何体的高的求解.试题解析:(1)证明:∵ DC
 平面ABC ,
平面ABC ,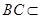 平面ABC
平面ABC ∴
 . .1分
. .1分∵AB是圆O的直径 ∴
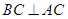 且
且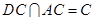
∴
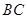
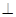 平面ADC. 3分
平面ADC. 3分∵四边形DCBE为平行四边形 ∴DE//BC
∴
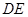
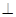 平面ADC 5分
平面ADC 5分又∵
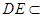 平面ADE ∴平面ACD
平面ADE ∴平面ACD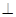 平面
平面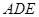 ..6分
..6分(2)所求简单组合体的体积:
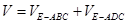
∵
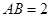 ,
,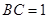 ,
, 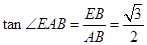
∴
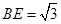 ,
,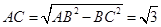 10分
10分∴

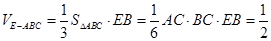
∴该简单几何体的体积
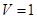 12分
12分
练习册系列答案
相关题目
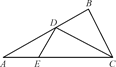 图①
图① 图②
图② A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=
A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF= AB.
AB.
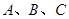 三点在球心为
三点在球心为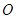 的球面上,
的球面上,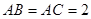 ,
,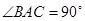 ,球心
,球心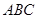 的距离为
的距离为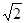 ,则球
,则球 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
 的半圆卷成一个圆锥,圆锥的体积为( )
的半圆卷成一个圆锥,圆锥的体积为( )


