题目内容
如图,四棱锥P ABCD中,PA⊥底面ABCD,PA=2
ABCD中,PA⊥底面ABCD,PA=2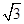 ,BC="CD=2," ∠ACB=∠ACD=
,BC="CD=2," ∠ACB=∠ACD=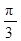 .
.
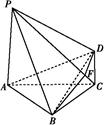
(1)求证:BD⊥平面PAC;
(2)若侧棱PC上的点F满足PF=7FC,求三棱锥P BDF的体积.
BDF的体积.
 ABCD中,PA⊥底面ABCD,PA=2
ABCD中,PA⊥底面ABCD,PA=2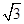 ,BC="CD=2," ∠ACB=∠ACD=
,BC="CD=2," ∠ACB=∠ACD=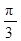 .
.
(1)求证:BD⊥平面PAC;
(2)若侧棱PC上的点F满足PF=7FC,求三棱锥P
 BDF的体积.
BDF的体积.(1)见解析 (2) 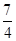
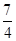
(1)证明:因为BC=CD,所以△BCD为等腰三角形,
又∠ACB=∠ACD,故BD⊥AC.
因为PA⊥底面ABCD,所以PA⊥BD.
从而BD与平面PAC内两条相交直线PA,AC都垂直,
所以BD⊥平面PAC.
(2)解:三棱锥P
 BCD的底面BCD的面积S△BCD=
BCD的底面BCD的面积S△BCD=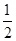 BC·CD·sin∠BCD=
BC·CD·sin∠BCD=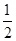 ×2×2×sin
×2×2×sin 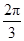 =
=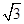 .
.由PA⊥底面ABCD,得
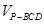 =
=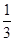 ·S△BCD·PA=
·S△BCD·PA=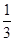 ×
×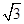 ×2
×2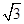 =2.
=2.由PF=7FC,得三棱锥F
 BCD的高为
BCD的高为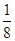 PA,
PA,故
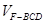 =
=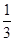 ·S△BCD·
·S△BCD·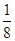 PA=
PA=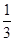 ×
×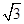 ×
×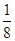 ×2
×2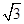 =
=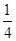 ,
,所以
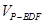 =
=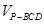 -
-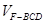 =2-
=2-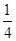 =
=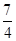 .
.
练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 图①
图① 图②
图② A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=
A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF= AB.
AB.
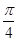 ,∠DAB=
,∠DAB=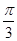 .沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:
.沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:
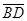 上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.
上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由. 是圆柱体
是圆柱体 的一条母线,
的一条母线, 过底面圆的圆心
过底面圆的圆心 ,
, 是圆
是圆 、
、 重合的任意一点,已知棱
重合的任意一点,已知棱 ,
, ,
, .
.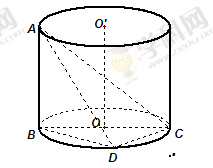
 ;
; 绕母线
绕母线 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.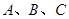 三点在球心为
三点在球心为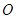 的球面上,
的球面上,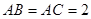 ,
,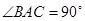 ,球心
,球心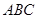 的距离为
的距离为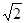 ,则球
,则球 ABC的体积为( )
ABC的体积为( )
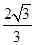
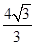
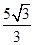
 A1B1C1D1的棱长为2,动点E,F在棱A1B1上,点Q是棱CD的中点,动点P在棱AD上.若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P
A1B1C1D1的棱长为2,动点E,F在棱A1B1上,点Q是棱CD的中点,动点P在棱AD上.若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P
 的半圆卷成一个圆锥,圆锥的体积为( )
的半圆卷成一个圆锥,圆锥的体积为( )


