题目内容
【题目】已知{e1,e2,e3}是空间的一个基底,且![]() =e1+2e2-e3,
=e1+2e2-e3,![]() =-3e1+e2+2e3,
=-3e1+e2+2e3,![]() =e1+e2-e3,试判断{
=e1+e2-e3,试判断{![]() }能否作为空间的一个基底?若能,试以此基底表示向量
}能否作为空间的一个基底?若能,试以此基底表示向量![]() =2e1-e2+3e3;若不能,请说明理由.
=2e1-e2+3e3;若不能,请说明理由.
【答案】能,![]() =17
=17![]() -5
-5![]() -30
-30![]() 。
。
【解析】
(1)假设![]() 共面,则
共面,则![]() =x
=x![]() +y
+y![]() 成立,
成立,![]()
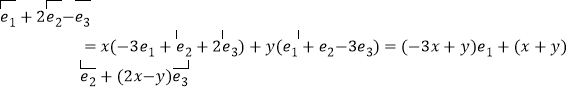
解方程组得方程组没有解,所以![]() 不共面,所以能作为空间的一个基底.(2) 设
不共面,所以能作为空间的一个基底.(2) 设![]() =p
=p![]() +q
+q![]() +z
+z![]() ,解方程组求出p,q,z得解.
,解方程组求出p,q,z得解.
能作为空间的一组基底。
假设![]() 共面,由向量共面的充要条件知存在实数x,y使
共面,由向量共面的充要条件知存在实数x,y使![]() =x
=x![]() +y
+y![]() 成立
成立
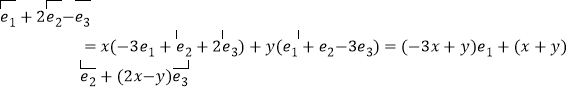
又因为![]() 是空间的一个基底,
是空间的一个基底,
所以![]() 不共面.
不共面.
因此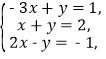 此方程组无解,
此方程组无解,
即不存在实数x,y使![]() =x
=x![]() +y
+y![]() ,
,
所以![]() 不共面.
不共面.
故{![]() }能作为空间的一个基底.
}能作为空间的一个基底.
设![]() =p
=p![]() +q
+q![]() +z
+z![]() ,
,
则有![]()
![]()
因为![]() 为空间的一个基底,
为空间的一个基底,
所以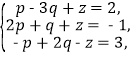 解得
解得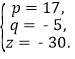
故![]() =17
=17![]() -5
-5![]() -30
-30![]() .
.

练习册系列答案
相关题目

