题目内容
【题目】设等差数列{an}的前n项和为Sn ， 且S4=4S2 ， a2+a4=10．
（1）求数列{an}通项公式；
（2）若数列{bn}满足 
+ 
+…+ 
=1﹣ 
，n∈N* ， 求数列{bn}的前n项和Tn ．
【答案】
（1）解：设等差数列{an}的公差为d，
∵a2+a4=10，
∴a3= 
=5，
∵S4=4S2，
∴4a3﹣2d=4（2a3﹣3d），
即20﹣2d=4（10﹣3d），解得：d=2，
∴an=a3+2（n﹣3）=2n﹣1；
（2）解：依题意， 
+ 
+…+ 
=1﹣ 
，n∈N*，
当n≥2时， + +…+ 
=1﹣ 
，
两式相减得： =（1﹣ ）﹣（1﹣ ）= ，
由（1）可知bn= 
（n≥2），
又∵b1=（1﹣ 
）a1= 满足上式，
∴bn= ，n∈N*，
故Tn= + 
+…+ ，
Tn= 
+ +…+ 
+ 
，
两式相减得： Tn= +（ + +…+ ）﹣
= 
﹣ ﹣ ，
∴Tn=3﹣ 
．
【解析】（1）通过设等差数列{an}的公差为d，利用等差中项及a2+a4=10可知a3=5，通过S4=4S2可知4a3﹣2d=4（2a3﹣3d），计算可得d=2，进而计算即得结论；（2）通过 + +…+ =1﹣ 与 + +…+ =1﹣ 作差，结合（1）整理可知bn= （n≥2），验证当n=1时也成立，进而利用错位相减法计算即得结论．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系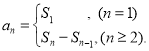
，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量
（吨）与相应的生产能耗
（吨）标准煤的几组对照数据：
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
（1）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（2）已知该厂技术改造前100吨甲产品能耗为90吨标准煤，试根据（1）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤？
（参考：
）
