题目内容
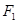 、
、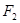 分别是双曲线
分别是双曲线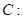
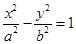
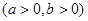 的左、右焦点,斜率为
的左、右焦点,斜率为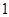 且过
且过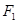 的直线
的直线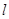 与
与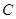 的右支交于点
的右支交于点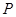 ,若
,若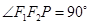 ,则双曲线
,则双曲线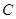 的离心率等于 .
的离心率等于 .
由斜率为1的直线的倾斜角为45°,且∠F1F2P=90°,得出三角形F1F2P是一个等腰三角形,从而有F1P=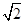 c,F2P=2c,再结合双曲线的定义,即能求出双曲线的离心率.
c,F2P=2c,再结合双曲线的定义,即能求出双曲线的离心率.
解答:解:在三角形F1F2P中,由题意得∠F1F2P=90°,又∠F1F2P=90°,
∴三角形F1F2P是一个等腰直角三角形,且F1F2=2c,
从而有F1P=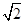 c,F2P=2c,
c,F2P=2c,
由双曲线定义F1P-F2P=2a得 2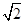 c-2c=2a,
c-2c=2a,
∴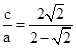 =1+
=1+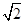 .
.
故答案为:1+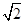 .
.
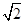 c,F2P=2c,再结合双曲线的定义,即能求出双曲线的离心率.
c,F2P=2c,再结合双曲线的定义,即能求出双曲线的离心率.解答:解:在三角形F1F2P中,由题意得∠F1F2P=90°,又∠F1F2P=90°,
∴三角形F1F2P是一个等腰直角三角形,且F1F2=2c,
从而有F1P=
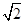 c,F2P=2c,
c,F2P=2c,由双曲线定义F1P-F2P=2a得 2
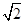 c-2c=2a,
c-2c=2a,∴
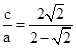 =1+
=1+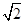 .
.故答案为:1+
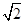 .
.
练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 及抛物线
及抛物线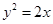 ,若抛物线上点
,若抛物线上点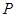 满足
满足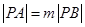 ,则
,则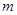
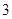
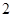
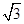
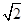
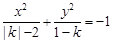 表示焦点在
表示焦点在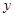 轴上的双曲线,那么它的半焦距
轴上的双曲线,那么它的半焦距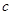 的取值范围是
的取值范围是 
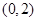
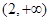
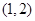
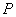 到点
到点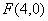 的距离比它到直线
的距离比它到直线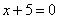 的距离小1,则
的距离小1,则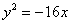

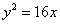
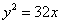
 中,设点
中,设点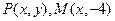 ,以线段
,以线段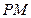 为直径的圆经过原点
为直径的圆经过原点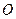 .
.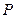 的轨迹
的轨迹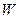 的方程;
的方程;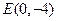 的直线
的直线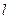 与轨迹
与轨迹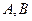 ,点
,点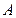 关于
关于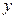 轴的对称点为
轴的对称点为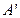 ,试判断直线
,试判断直线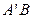 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论.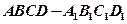 中,
中,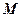 为
为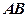 的中点,P是平面
的中点,P是平面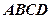 内的动点,且满足条件
内的动点,且满足条件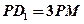 ,则动点P在平面
,则动点P在平面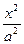 -
-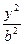 =1(a>0,b>0)的焦点,而且被该双曲线的右准线分成的弧长为2∶1的两段圆弧,那么该双曲线的离心率e等于
=1(a>0,b>0)的焦点,而且被该双曲线的右准线分成的弧长为2∶1的两段圆弧,那么该双曲线的离心率e等于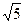
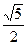

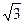
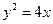 上一动点,则点P到y轴距离和到点A
上一动点,则点P到y轴距离和到点A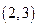 距离之和的最小值等于 .
距离之和的最小值等于 .