题目内容
在平面直角坐标系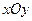 中,设点
中,设点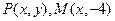 ,以线段
,以线段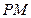 为直径的圆经过原点
为直径的圆经过原点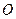 .
.
(Ⅰ)求动点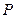 的轨迹
的轨迹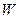 的方程;
的方程;
(Ⅱ)过点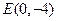 的直线
的直线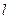 与轨迹
与轨迹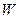 交于两点
交于两点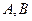 ,点
,点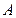 关于
关于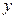 轴的对称点为
轴的对称点为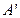 ,试判断直线
,试判断直线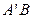 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论.
 中,设点
中,设点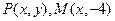 ,以线段
,以线段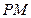 为直径的圆经过原点
为直径的圆经过原点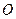 .
.(Ⅰ)求动点
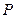 的轨迹
的轨迹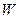 的方程;
的方程;(Ⅱ)过点
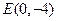 的直线
的直线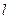 与轨迹
与轨迹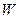 交于两点
交于两点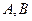 ,点
,点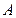 关于
关于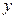 轴的对称点为
轴的对称点为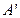 ,试判断直线
,试判断直线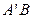 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论.解:(I)由题意可得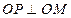 , ……………………………2分
, ……………………………2分
所以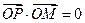 ,即
,即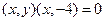 ……………………………4分
……………………………4分
即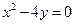 ,即动点
,即动点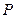 的轨迹
的轨迹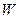 的方程为
的方程为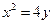 …………5分
…………5分
(II)设直线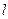 的方程为
的方程为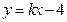 ,
,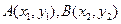 ,则
,则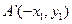 .
.
由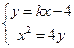 消
消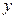 整理得
整理得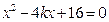 , ………………………………6分
, ………………………………6分
则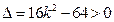 ,即
,即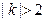 . ………………………………7分
. ………………………………7分
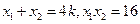 . …………………………………9分
. …………………………………9分
直线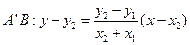
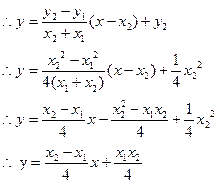 …………………………12分
…………………………12分
即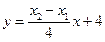
所以,直线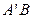 恒过定点
恒过定点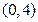 . ……………………13分
. ……………………13分
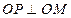 , ……………………………2分
, ……………………………2分所以
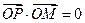 ,即
,即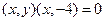 ……………………………4分
……………………………4分即
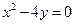 ,即动点
,即动点 的轨迹
的轨迹 的方程为
的方程为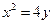 …………5分
…………5分(II)设直线
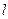 的方程为
的方程为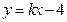 ,
,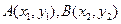 ,则
,则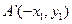 .
.由
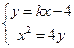 消
消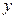 整理得
整理得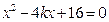 , ………………………………6分
, ………………………………6分则
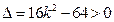 ,即
,即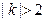 . ………………………………7分
. ………………………………7分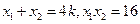 . …………………………………9分
. …………………………………9分直线
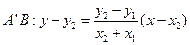
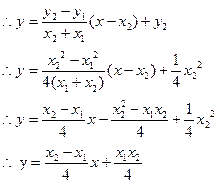 …………………………12分
…………………………12分即
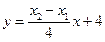
所以,直线
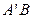 恒过定点
恒过定点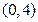 . ……………………13分
. ……………………13分略

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
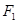 、
、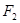 分别是双曲线
分别是双曲线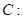
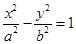
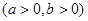 的左、右焦点,斜率为
的左、右焦点,斜率为 且过
且过 与
与 的右支交于点
的右支交于点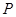 ,若
,若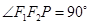 ,则双曲线
,则双曲线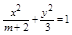 的焦点在x轴上,且离心率e=
的焦点在x轴上,且离心率e=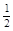 ,则m的值为( )
,则m的值为( )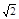
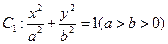 的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线
的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线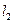 垂直
垂直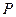 ,线段
,线段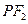 垂直平分线交
垂直平分线交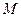
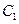 的标准方程和动点
的标准方程和动点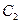 的方程。
的方程。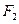 作斜率为1的直线交椭圆于A、B两点,求
作斜率为1的直线交椭圆于A、B两点,求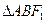 的面积。
的面积。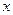 轴交于点
轴交于点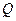 ,不同的两点
,不同的两点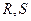 在轨迹
在轨迹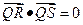 求证:直线
求证:直线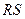 恒过
恒过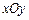 中,
中,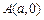
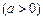 ,
,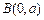 ,
,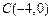 ,
,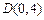 ,设
,设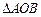 的外接圆圆心为E.
的外接圆圆心为E.
 (1)若⊙E与直线CD相切,求实数a的值;
(1)若⊙E与直线CD相切,求实数a的值;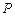 在圆
在圆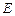 上,使
上,使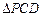 的面积等于12的点
的面积等于12的点
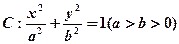 的焦距为2,点
的焦距为2,点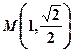 在椭圆
在椭圆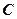 上,
上,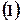 求椭圆
求椭圆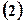 若过点
若过点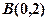 的直线与
的直线与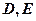 (
(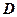 在
在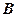 、
、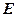 之间);
之间);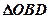 与
与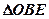 面积之比的取值范围.
面积之比的取值范围.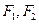 ,离心率为
,离心率为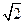 ,且过点
,且过点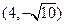 ,
,
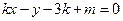 (其中
(其中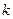 为参数)所过的定点
为参数)所过的定点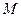 恰在双曲线上,求证:
恰在双曲线上,求证: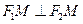 。
。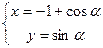
 上任意一点,则(x-2)2+(x+4)2的最大值是
上任意一点,则(x-2)2+(x+4)2的最大值是