Question

【题目】抛物线y=﹣x2+2x与x轴围成的封闭区域为M，向M内随机投掷一点P（x，y），则P（y＞x）= ．

Answer 1

【答案】
【解析】解：令y=﹣x2+2x=0，解得x=0或x=2， ∴由抛物线y=﹣x2+2x与x轴围成的封闭区域SM= （﹣x2+2x）dx=（﹣ x3+x2）| =﹣ +4= ，
由 ，解得x=0或x=1，
∴由抛物线y=﹣x2+2x与y=x围成的封闭区域
S阴影= （（﹣x2+2x﹣x）dx= （（﹣x2+x）dx=（﹣ x3+ x2）| =﹣ + = ，
故则P（y＞x）= = = ，
所以答案是：

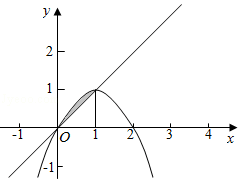
【考点精析】通过灵活运用几何概型，掌握几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等即可以解答此题．