题目内容
【题目】如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,FD⊥平面ABCD, ![]() .
. 
(I)求证:EF∥平面ABCD;
(II)求证:平面ACF⊥平面BDF.
【答案】证明:(Ⅰ)如图,过点E作EH⊥BC于H,连接HD,∴ ![]() . ∵平面ABCD⊥平面BCE,EH平面BCE,
. ∵平面ABCD⊥平面BCE,EH平面BCE,
平面ABCD∩平面BCE=BC,
∴EH⊥平面ABCD,
又∵FD⊥平面ABCD, ![]() ,
,
∴FD∥EH,FD=EH.
∴四边形EHDF为平行四边形.
∴EF∥HD.
∵EF平面ABCD,HD平面ABCD,
∴EF∥平面ABCD. …
(Ⅱ)∵FD⊥面ABCD,∴FD⊥AC,
又四边形ABCD是菱形,∴AC⊥BD,
又FD∩BD=D,∴AC⊥面FBD,
又AC面ACF,从而面ACF⊥面BDF.…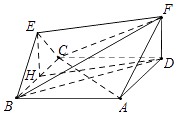
【解析】(Ⅰ)如图,过点E作EH⊥BC于H,连接HD,证明四边形EHDF为平行四边形,根据线面平行的判定定理即可证明EF∥平面ABCD;(Ⅱ)证明AC⊥面FBD,即可证明平面ACF⊥平面BDF.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对平面与平面垂直的判定的理解,了解一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目