题目内容
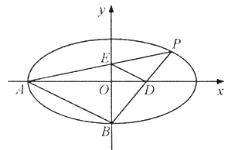
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,焦点到相应准线的距离为
,焦点到相应准线的距离为![]() ,
,![]() ,
,![]() 分别为椭圆的左顶点和下顶点,
分别为椭圆的左顶点和下顶点,![]() 为椭圆
为椭圆![]() 上位于第一象限内的一点,
上位于第一象限内的一点,![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)求证:四边形![]() 的面积为定值.
的面积为定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】分析:(1)直接根据原题得到![]() ,
,![]() ,解方程组即得椭圆
,解方程组即得椭圆![]() 的标准方程.(2)先求出
的标准方程.(2)先求出![]() ,再求
,再求![]() 的值.(3) 设
的值.(3) 设![]() ,先求出四边形
,先求出四边形![]() 的面积
的面积![]() ,再化简得到四边形
,再化简得到四边形![]() 的面积为定值.
的面积为定值.
详解:(1)设右焦点![]() ,因为椭圆
,因为椭圆![]() 的离心率为
的离心率为![]() ,所以
,所以![]() ,①
,①
又因为右焦点![]() 到右准线的距离为
到右准线的距离为![]() ,所以
,所以![]() ,②
,②
由①②得,![]() ,
,![]() ,
,![]() ,
,
所以椭圆![]() 的标准方程是
的标准方程是![]() .
.
(2)因为![]() ,所以
,所以![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
由 ,得
,得![]() ,解得
,解得![]() (舍)或
(舍)或![]() ,
,
可得![]() ,
,
直线![]() 的方程为
的方程为![]() ,令
,令![]() ,得
,得![]() ,
,
所以![]() .
.
(3)设![]() ,则
,则![]() ,即
,即![]() .
.
直线![]() 的方程为
的方程为![]() ,令
,令![]() ,得
,得![]() .
.
直线![]() 的方程为
的方程为![]() ,令
,令![]() ,得
,得![]() .
.
所以四边形![]() 的面积
的面积![]()
![]()
![]()
![]() 为定值.
为定值.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
【题目】为了调查某中学学生在周日上网的时间,随机对![]() 名男生和
名男生和![]() 名女生进行了不记名的问卷调查,得到了如下的统计结果:
名女生进行了不记名的问卷调查,得到了如下的统计结果:
表1:男、女生上网时间与频数分布表
上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
男生人数 | 5 | 25 | 30 | 25 | 15 |
女生人数 | 10 | 20 | 40 | 20 | 10 |
(Ⅰ)若该中学共有女生750人,试估计其中上网时间不少于60分钟的人数;
(Ⅱ)完成下表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
男生 | |||
女生 | |||
合计 |
附:公式![]() ,其中
,其中![]()
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |