题目内容
我们常用定义解决与圆锥曲线有关的问题.如“设椭圆
+
=1(a>0,b>0)的左、右焦点分别为F1,F2,过左焦点F1作倾斜角为θ的弦AB,设|F1A|=r1,|F1B|=r2,试证
+
为定值”.
证明如下:不妨设A在x轴的上方,在△ABC中,由椭圆的定义及余弦定理得,(2a-r1)2=r12+4c2-4cr1cosθ,∴r1=
,
同理r2=
=
,于是
1+
2=
.请用类似的方法探索:设双曲线
-
=1(a>0,b>0)的左、右焦点分别为F1,F2,过左焦点F1作倾斜角为θ的直线与双曲线右支交于点A,左支交于点B,设|F1A|=r1,|F1B|=r2,是否有类似的结论成立,请写出与定值有关的结论是______..
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| r1 |
| 1 |
| r2 |
证明如下:不妨设A在x轴的上方,在△ABC中,由椭圆的定义及余弦定理得,(2a-r1)2=r12+4c2-4cr1cosθ,∴r1=
| b2 |
| a-ccosθ |
同理r2=
| b2 |
| a-ccos(π-θ) |
| b2 |
| a+ccosθ |
| 1 |
| r |
| 1 |
| r |
| 2a |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
由题意,根据椭圆的定义与双曲线的定义类比得“设双曲线
-
=1(a>0,b>0)的左、右焦点分别为F1,F2,过左焦点F1作倾斜角为θ的直线与双曲线右支交于点A,左支交于点B,设|F1A|=r1,|F1B|=r2,试证
1-
2为定值”,证明如下:
不妨设A在x轴的上方,令在△ABC中,由双曲线的定义及余弦定理得,(2a+r1)2=r12+4c2+4cr1cosθ,
∴r1=
,
同理r2=
=
,
于是
1-
2=-
.
故答案为
1-
2=-
.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| r |
| 1 |
| r |
不妨设A在x轴的上方,令在△ABC中,由双曲线的定义及余弦定理得,(2a+r1)2=r12+4c2+4cr1cosθ,
∴r1=
| b2 |
| a+ccosθ |
同理r2=
| b2 |
| a+ccos(π-θ) |
| b2 |
| a+ccosθ |
于是
| 1 |
| r |
| 1 |
| r |
| 2a |
| b2 |
故答案为
| 1 |
| r |
| 1 |
| r |
| 2a |
| b2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
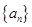 满足a1=0且
满足a1=0且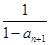 -
-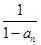 = 1.
= 1.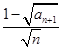 ,记Sn=
,记Sn=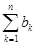 ,证明:Sn<1.
,证明:Sn<1.
 为实数,则方程
为实数,则方程 至少有一个实根”时,要做的假设是( )
至少有一个实根”时,要做的假设是( ) 中得出的一般性结论是_____________。
中得出的一般性结论是_____________。