题目内容
已知函数f(n)=log(n+1)(n+2)(n∈N*)，若存在正整数k满足：f（1）•f（2）•f（3）•…•f（n）=k，那么我们把k叫做关于n的“对整数”，则当n∈[1，10]时，“对整数”共有（ ）
| A．1个 | B．2个 | C．4个 | D．8个 |
由题意，根据换底公式得，f（x）=log（x+1） （x+2）=
，
所以k=f（1）f（2）f（3）…f（x）=
•
•
…
=
=log2（x+2）．
∵1≤x≤10，∴log23≤log2（x+2）≤log212
整数有log24，log28，即2，3，两个整数．
故选：B．
| lg(x+2) |
| lg(x+1) |
所以k=f（1）f（2）f（3）…f（x）=
| lg3 |
| lg2 |
| lg4 |
| lg3 |
| lg5 |
| lg4 |
| lg(x+2) |
| lg(x+1) |
| lg(x+2) |
| lg2 |
∵1≤x≤10，∴log23≤log2（x+2）≤log212
整数有log24，log28，即2，3，两个整数．
故选：B．
练习册系列答案
天天练口算系列答案
相关题目
，试证明
至少有一个不小于1.
.
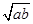的最小值是（ ）
