题目内容
18．函数y=$\frac{1}{co{s}^{2}x}$+$\frac{1}{si{n}^{2}x}$的最小值为4．分析 化简函数y=$\frac{1}{co{s}^{2}x}$+$\frac{1}{si{n}^{2}x}$=$\frac{4}{si{n}^{2}2x}$，利用三角函数的单调性值域即可得出．
解答 解：函数y=$\frac{1}{co{s}^{2}x}$+$\frac{1}{si{n}^{2}x}$=$\frac{4}{si{n}^{2}2x}$≥4，当且仅当sin2x=±1时取等号．
故答案为：4．
点评 本题考查了三角函数的单调性值域，属于基础题．
练习册系列答案
相关题目
6．若函数f（x）=log${\;}_{\frac{1}{2}}$（-x2+4x+5）在区间（3m-2，m+2）内单调递增，则实数m的取值为（ ）
| A． | [$\frac{4}{3}，3$] | B． | [$\frac{4}{3}，2$] | C． | [$\frac{4}{3}，2$） | D． | [$\frac{4}{3}，+∞$） |
13．已知集合A={x|x2-2x-3≤0}，B={x|x＜a}，若A⊆B，则实数a的取值范围是（ ）
| A． | （-1，+∞） | B． | [-1，+∞） | C． | （3，+∞） | D． | [3，+∞） |
3．某几何体的三视图如图所示，则该几何体的体积为（ ）
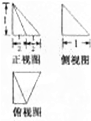
| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |