题目内容
【题目】已知
是抛物线
上位于
轴两侧的不同两点
（1）若
在直线
上，且使得以
为顶点的四边形恰为正方形，求该正方形的面积.
（2）求过
、
的切线与直线
围成的三角形面积的最小值；
【答案】（1）
或
；（2）
【解析】
(1)联解直线方程和抛物线方程，可求出
的弦长
，再结合已知条件以
为顶点的四边形为正方形可得到正方形的边长，从而可求得面积；
(2)分别求出切线方程，由切线方程求出交点坐标，代入三角形的面积公式，利用基本不等式求出面积的最小值.
（1）设直线
联立直线与抛物线方程得：
易得：
直线与
之间的距离为
令
，可得
所以该正方形的边长为
或
面积为或；
（2）设
，
（由对称性不妨设
）
则
处的切线方程为：
，与直线
交点记为M，则
则
处的切线方程为：
，与直线交点记为N，则
两条切线交点P
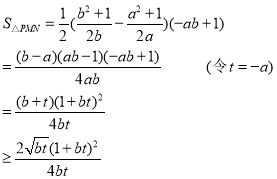
于是
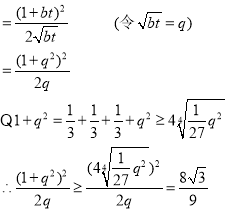
当
时取到等号
所以该三角形面积的最小值为
【题目】某汽车品牌为了了解客户对于其旗下的五种型号汽车的满意情况，随机抽取了一些客户进行回访，调查结果如下表：
汽车型号 | I | II | III | IV | V |
回访客户（人数） | 250 | 100 | 200 | 700 | 350 |
满意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
满意率是指：某种型号汽车的回访客户中，满意人数与总人数的比值.
假设客户是否满意互相独立，且每种型号汽车客户对于此型号汽车满意的概率与表格中该型号汽车的满意率相等.
(1)从所有的回访客户中随机抽取1人，求这个客户满意的概率；
(2)从I型号和V型号汽车的所有客户中各随机抽取1人，设其中满意的人数为
，求的分布列和期望；
(3)用 “
”, “
”, “
”, “
”, “
”分别表示I, II, III, IV, V型号汽车让客户满意， “
”, “
”, “
”, “
”, “
” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差
的大小关系.
【题目】随着手机的发展，“微信”逐渐成为人们支付购物的一种形式.某机构对“使用微信支付”的态度进行调查，随机抽取了50人，他们年龄的频数分布及对“使用微信支付”赞成人数如下表.
年龄 （单位：岁） |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
（Ⅰ）若以“年龄45岁为分界点”，由以上计数据完成下面
列联表，并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关；
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
（Ⅱ）若从年龄在
的被调查人中按照赞成与不赞成分层抽样，抽取5人进行追踪调查，在5人中抽取3人做专访，求3人中不赞成使用微信支付的人数的分布列和期望值.
参考数据：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
，其中
.
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量，某城市环保局随机抽取了一年内100天的空气质量指数（
）的检测数据，结果统计如下：
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 6 | 14 | 18 | 27 | 25 | 10 |
（1）从空气质量指数属于
，
的天数中任取3天，求这3天中空气质量至少有2天为优的概率；
（2）已知某企业每天的经济损失
（单位：元）与空气质量指数
的关系式为
，试估计该企业一个月（按30天计算）的经济损失的数学期望.