题目内容
20.在平面直角坐标系xOy中,已知直线y=x与圆心在第二象限的圆C相切于原点O,且圆C与圆C′:x2+y2-2x-2y-6=0的面积相等.(Ⅰ)求圆C的标准方程;
(Ⅱ)试探究圆C上是否存在异于原点的点Q,使点Q到定点F(4,0)的距离等于线段OF的长?若存在,求出点Q的坐标;若不存在,请说明理由.
分析 (Ⅰ)由圆C与圆C′:x2+y2-2x-2y-6=0的面积相等,得到圆C的半径r=2$\sqrt{2}$,设圆C的圆心为C(a,b),由已知得点O(0,0)在圆C上,且OC垂直于直线y=x,由此能求出圆心C(a,b),从而能求出圆C的方程.
(Ⅱ)假设存在点Q满足题意,设Q(x,y),则由点Q在圆C上且点Q到定点F(4,0)的距离等于线段OF的长列出方程组,由此能求出存在点Q,使点Q到定点F(4,0)的距离等于线段OF的长.
解答 解:(Ⅰ)圆C′:x2+y2-2x-2y-6=0的方程转化为(x-1)2+(y-1)2=8,(2分)
∵圆C与圆C′:x2+y2-2x-2y-6=0的面积相等,∴两圆的半径相等,∴圆C的半径r=2$\sqrt{2}$,
设圆C的圆心为C(a,b),则圆C的方程为(x-a)2+(y-b)2=8,
∵直线y=x与圆心在第二象限的圆C相切于原点O,
∴点O(0,0)在圆C上,且OC垂直于直线y=x,
∴$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=8}\\{\frac{b}{a}=-1}\end{array}\right.$,解得a=2,b=-2或a=-2,b=2,
∵点C(a,b)在第二象限,∴a<0,b>0,∴a=-2,b=2,
∴圆C的方程为(x+2)2+(y-2)2=8.(6分)
(Ⅱ)假设存在点Q满足题意,设Q(x,y),则有$\left\{\begin{array}{l}{(x-4)^{2}+{y}^{2}=16}\\{(x+2)^{2}+(y-2)^{2}=8}\end{array}\right.$,(8分)
解得$\left\{\begin{array}{l}{x=\frac{4}{5}}\\{y=\frac{12}{5}}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$(舍),
∴存在点Q($\frac{4}{5},\frac{12}{5}$),使点Q到定点F(4,0)的距离等于线段OF的长.(12分)
点评 本题考查圆的方程的求法,考查满足条件的点是否存在的判断,是中档题,解题时要认真审题,注意圆的方程、两点间距离公式的合理运用.

| A. | 4 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
m(件)与时间t(天)的关系如表所示.
| 时间t/天 | 1 | 3 | 6 | 10 | 36 | … |
| 日销售量 m/件 | 94 | 90 | 84 | 76 | 24 | … |
(1)认真分析表格中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些 数据的m(件)与t(天)的关系式.
(2)试预测未来40天中哪一天的日销售利润最大,最大利润是多少?
(3)在实际销售的前20天中,该公司决定每销售1件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
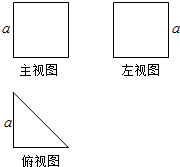 已知某个几何体的三视图如图,其中主视图和左视图(侧视图)都是边长为a的正方形,俯视图是直角边长为a的等腰直角三角形,则此几何体的表面积为( )
已知某个几何体的三视图如图,其中主视图和左视图(侧视图)都是边长为a的正方形,俯视图是直角边长为a的等腰直角三角形,则此几何体的表面积为( )| A. | (3+$\sqrt{2}$)a2 | B. | 4a2 | C. | (4+$\sqrt{2}$)a2 | D. | 3$\sqrt{2}$a2 |
| X | 0 | 1 | 2 | 3 |
| p | 0.1 | 0.3 | 0.4 | 0.2 |
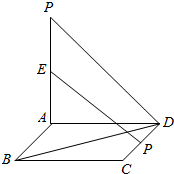 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.