题目内容
13.一艘船以20km/h的速度向正北航行,船在A处看见灯塔B在船的东北方向,1h后船在C处看见灯塔B在船的北偏东75°的方向上,这时船与灯塔的距离BC等于( )| A. | 20$\sqrt{2}$ | B. | 20 | C. | 20$\sqrt{3}$ | D. | 10$\sqrt{2}$ |
分析 由题意画出图形:∠A=45°,∠ACB=105°,推出∠B,求出AC,利用三角形求出CD,然后求BC.
解答 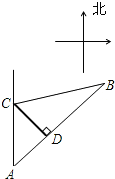 解:由题意画出图形,如图过C作CD⊥AB于D,
解:由题意画出图形,如图过C作CD⊥AB于D,
在Rt△ACD中,AC=20×1=20,∠A=45°,
∴sinA=$\frac{CD}{AC}$.
∴CD=AC•sinA=20×$\frac{\sqrt{2}}{2}$=10$\sqrt{2}$.
在Rt△BCD中,∠B=∠PCB-∠A=75°-45°=30°,
∴BC=2•CD=2×10$\sqrt{2}$=20$\sqrt{2}$(n mile).
∴此时船与灯塔的距离BC为20$\sqrt{2}$n mile.
故选:A.
点评 本题考查三角形的实际应用,转化思想的应用,考查计算能力,属于中档题.

练习册系列答案
相关题目
4.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的两个焦点,若双曲线上存在一点P,使得|PF1|,2a,|PF2|成等差数列,则双曲线离心率的取值范围是( )
| A. | (1,2) | B. | (1,2] | C. | [2,+∞) | D. | (2,+∞) |
5.红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量
m(件)与时间t(天)的关系如表所示.
未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为y1=$\frac{1}{4}$t+25(1≤t≤20,且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系为y2=$\frac{1}{2}$t+40(21≤t≤40,且t为整数).下面我们就来研究销售这种商品的有关问题.
(1)认真分析表格中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些 数据的m(件)与t(天)的关系式.
(2)试预测未来40天中哪一天的日销售利润最大,最大利润是多少?
(3)在实际销售的前20天中,该公司决定每销售1件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
m(件)与时间t(天)的关系如表所示.
| 时间t/天 | 1 | 3 | 6 | 10 | 36 | … |
| 日销售量 m/件 | 94 | 90 | 84 | 76 | 24 | … |
(1)认真分析表格中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些 数据的m(件)与t(天)的关系式.
(2)试预测未来40天中哪一天的日销售利润最大,最大利润是多少?
(3)在实际销售的前20天中,该公司决定每销售1件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
2.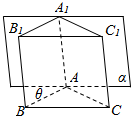 已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的值不可能是( )
已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的值不可能是( )
 已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的值不可能是( )
已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的值不可能是( )| A. | $\sqrt{3}$ | B. | 4 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{2}$ |

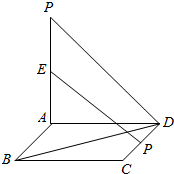 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.