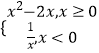题目内容
【题目】
已知函数f(x)=2x3-3(a+1)x2+6ax,a∈R.
(Ⅰ)曲线y=f(x)在x=0处的切线的斜率为3,求a的值;
(Ⅱ)若对于任意x∈(0,+∞),f(x)+f(-x)≥12lnx恒成立,求a的取值范围;
(Ⅲ)若a>1,设函数f(x)在区间[1,2]上的最大值、最小值分别为M(a)、m(a),
记h(a)=M(a)-m(a),求h(a)的最小值.
【答案】(1)![]() (2)(-∞,-1-
(2)(-∞,-1-![]() ](3)
](3)![]()
【解析】试题分析:(1)求出![]() ,由
,由![]() 可得结果;(2)对于任意
可得结果;(2)对于任意![]() 恒成立等价于
恒成立等价于![]() ,利用导数研究函数的单调性,求得
,利用导数研究函数的单调性,求得![]() ,从而可得结果;(3)分三种情况讨论:①当
,从而可得结果;(3)分三种情况讨论:①当![]() ,②当
,②当![]() ,③当
,③当![]() 分别求出
分别求出![]() 的最小值,再比较大小即可得结果.
的最小值,再比较大小即可得结果.
试题解析:(1)因为f(x)=2x3-3(a+1)x2+6ax,所以f ′(x)=6x2-6(a+1)x+6a,
所以曲线y=f(x)在x=0处的切线斜率k=f ′(0)=6a,
所以6a=3,所以a=![]() .
.
(2)f(x)+f(-x)=-6(a+1)x2≥12lnx对任意x∈(0,+∞)恒成立,
所以-(a+1)≥![]() .
.
令g(x)=![]() ,x>0,则g(x)=
,x>0,则g(x)=![]() .
.
令g(x)=0,解得x=![]() .
.
当x∈(0,![]() )时,g(x)>0,所以g(x)在(0,
)时,g(x)>0,所以g(x)在(0,![]() )上单调递增;
)上单调递增;
当x∈(![]() ,+∞)时,g(x)<0,所以g(x)在(
,+∞)时,g(x)<0,所以g(x)在(![]() ,+∞)上单调递减.
,+∞)上单调递减.
所以g(x)max=g(![]() )=
)=![]() ,
,
所以-(a+1)≥![]() ,即a≤-1-
,即a≤-1-![]() ,
,
所以a的取值范围为(-∞,-1-![]() ].
].
(3)因为f(x)=2x3-3(a+1)x2+6ax,
所以f ′(x)=6x2-6(a+1)x+6a=6(x-1)(x-a),f(1)=3a-1,f(2)=4.
令f ′(x)=0,则x=1或a.
f(1)=3a-1,f(2)=4.
①当1<a≤![]() 时,
时,
当x∈(1,a)时,f (x)<0,所以f(x)在(1,a)上单调递减;
当x∈(a,2)时,f (x)>0,所以f(x)在(a,2)上单调递增.
又因为f(1)≤f(2),所以M(a)=f(2)=4,m(a)=f(a)=-a3+3a2,
所以h(a)=M(a)-m(a)=4-(-a3+3a2)=a3-3a2+4.
因为h (a)=3a2-6a=3a(a-2)<0,
所以h(a)在(1,![]() ]上单调递减,
]上单调递减,
所以当a∈(1,![]() ]时,h(a)最小值为h(
]时,h(a)最小值为h(![]() )=
)=![]() .
.
②当![]() <a<2时,
<a<2时,
当x∈(1,a)时,f (x)<0,所以f(x)在(1,a)上单调递减;
当x∈(a,2)时,f (x)>0,所以f(x)在(a,2)上单调递增.
又因为f(1)>f(2),所以M(a)=f(1)=3a-1,m(a)=f(a)=-a3+3a2,
所以h(a)=M(a)-m(a)=3a-1-(-a3+3a2)=a3-3a2+3a-1.
因为h (a)=3a2-6a+3=3(a-1)2≥0.
所以h(a)在( ,2)上单调递增,
,2)上单调递增,
所以当a∈(![]() ,2)时,h(a)>h(
,2)时,h(a)>h(![]() )=
)=![]() .
.
③当a≥2时,
当x∈(1,2)时,f (x)<0,所以f(x)在(1,2)上单调递减,
所以M(a)=f(1)=3a-1,m(a)=f(2)=4,
所以h(a)=M(a)-m(a)=3a-1-4=3a-5,
所以h(a)在[2,+∞)上的最小值为h(2)=1.
综上,h(a)的最小值为![]() .
.
【方法点晴】本题主要考查导数的几何意义、利用导数求函数的最值以及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 数形结合(
即可);② 数形结合(![]() 图象在
图象在![]() 上方即可);③ 讨论最值
上方即可);③ 讨论最值![]() 或
或![]() 恒成立;④ 讨论参数.
恒成立;④ 讨论参数.