题目内容
【题目】若函数 ,关于x的方程
,关于x的方程![]() 有3个不同的实数根,则( )
有3个不同的实数根,则( )
A. b<﹣2且c>0B. b>﹣2且c<0C. b=﹣2且c=0D. b>﹣2且c=0
【答案】C
【解析】
令t=f(x),由关于x的方程![]() 可化为t2+bt+c=0,设关于t的方程有两根为t=t1,t=t2,由关于x的方程
可化为t2+bt+c=0,设关于t的方程有两根为t=t1,t=t2,由关于x的方程![]() 有3个不同的实数根可转化为函数t=f(x)的图象与直线t=t1,t=t2的交点个数为3个,作出
有3个不同的实数根可转化为函数t=f(x)的图象与直线t=t1,t=t2的交点个数为3个,作出![]() 的简图,利用图象特征可得:t1=2,t2=0,再利用韦达定理列方程得解。
的简图,利用图象特征可得:t1=2,t2=0,再利用韦达定理列方程得解。
解:令t=f(x),
则t2+bt+c=0,
设关于t的方程有两根为t=t1,t=t2,
关于x的方程![]() 有3个不同的实数根等价于函数t=f(x)的图象与直线t=t1,t=t2的交点个数为3个,
有3个不同的实数根等价于函数t=f(x)的图象与直线t=t1,t=t2的交点个数为3个,
作出![]() 的简图如下:
的简图如下:
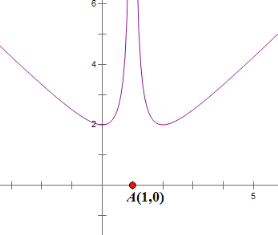
由函数t=f(x)的图象与直线t=t1,t=t2的位置关系可得:
t1=2,t2=0,
由韦达定理可得:
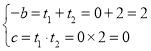 ,即b=﹣2,c=0,
,即b=﹣2,c=0,
故选:C.

 阅读快车系列答案
阅读快车系列答案【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(Ⅰ)求一续保人本年度的保费高于基本保费的概率;
(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出![]() 的概率;
的概率;
(Ⅲ)求续保人本年度的平均保费与基本保费的比值.
【题目】在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
1 | 2 | 3 | 4 | 5 | |
价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知![]() ,
,
(1)画出散点图;
(2)求出y对x的线性回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).
参考公式:
![]() .
.
