题目内容
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且
,且![]() ,圆
,圆![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() ,
,![]() 面积最大值为
面积最大值为![]() .
.
(1)求圆![]() 与椭圆
与椭圆![]() 的方程;
的方程;
(2)圆![]() 的切线
的切线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .;(2)
.;(2)![]() .
.
【解析】分析:(1)由题意结合几何关系得到关于a,b,c的方程组,求解方程组可得![]() ,
,![]() ,
,![]() .则圆
.则圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(2)①当直线![]() 的斜率不存在时,计算可得
的斜率不存在时,计算可得![]() .
.
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() 利用圆心到直线的距离等于半径可得
利用圆心到直线的距离等于半径可得![]() ,联立直线与椭圆方程可得
,联立直线与椭圆方程可得![]() ,由弦长公式有
,由弦长公式有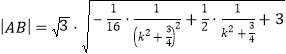 .令
.令![]() ,换元后结合二次函数的性质可得
,换元后结合二次函数的性质可得![]() .则
.则![]() 的取值范围是
的取值范围是![]() .
.
详解:(1)因为![]() ,所以
,所以![]() .①
.①
因为![]() ,所以点
,所以点![]() 为椭圆的焦点,所以
为椭圆的焦点,所以![]() .
.
设![]() ,则
,则![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ,②
,②
由①,②解得![]() ,所以
,所以![]() ,
,![]() .
.
所以圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(2)①当直线![]() 的斜率不存在时,不妨取直线
的斜率不存在时,不妨取直线![]() 的方程为
的方程为![]() ,解得
,解得![]() .
.
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
因为直线![]() 与圆相切,所以
与圆相切,所以![]() ,即
,即![]() ,
,
联立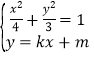 ,消去
,消去![]() 可得
可得![]() ,
,
![]() .
.
![]()
=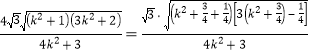
=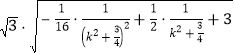 .
.
令![]() ,则
,则![]() ,所以
,所以![]() =
=![]() ,
,
所以![]() =
=![]() ,所以
,所以![]() .
.
综上,![]() 的取值范围是
的取值范围是![]() .
.

【题目】(Ⅰ)如表所示是某市最近5年个人年平均收入表节选.求y关于x的回归直线方程,并估计第6年该市的个人年平均收入(保留三位有效数字).
年份x | 1 | 2 | 3 | 4 | 5 |
收入y(千元) | 21 | 24 | 27 | 29 | 31 |
其中![]() ,
,![]() ,
,![]() 附1:
附1:![]() =
= ![]() ,
,![]() =
=![]() ﹣
﹣![]()
![]()
(Ⅱ)下表是从调查某行业个人平均收入与接受专业培训时间关系得到2×2列联表:
受培时间一年以上 | 受培时间不足一年 | 总计 | |
收入不低于平均值 | 60 | 20 | |
收入低于平均值 | 10 | 20 | |
总计 | 100 |
完成上表,并回答:能否在犯错概率不超过0.05的前提下认为“收入与接受培训时间有关系”.
附2:
P(K2≥k0) | 0.50 | 0.40 | 0.10 | 0.05 | 0.01 | 0.005 |
k0 | 0.455 | 0.708 | 2.706 | 3.841 | 6.635 | 7.879 |
附3:
K2=![]() .(n=a+b+c+d)
.(n=a+b+c+d)
【题目】保险公司统计的资料表明:居民住宅区到最近消防站的距离x(单位:千米)和火灾所造成的损失数额y(单位:千元)有如下的统计资料:
距消防站距离x(千米) | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
火灾损失费用y(千元) | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明y与x有线性相关关系,试求:
(Ⅰ)求相关系数![]() (精确到0.01);
(精确到0.01);
(Ⅱ)求线性回归方程(精确到0.01);
(III)若发生火灾的某居民区与最近的消防站相距10.0千米,评估一下火灾的损失(精确到0.01).
参考数据:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
参考公式:相关系数  ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]()

