题目内容
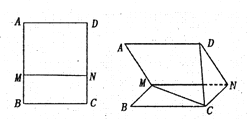
【题目】如图，矩形
所在平面与以
为直径的圆所在平面垂直，
为中点，
是圆周上一点，且
，
，
．
（1）求异面直线
与
所成角的余弦值；
（2）设点
是线段
上的点，且满足
，若直线
平面
，求实数
的值．
【答案】（1）
；（2）1
【解析】
（1）取
中点
，连接
，即
为所求角。在
中，易得MC，NC的长，MN可在直角三角形
中求得。再用余弦定理易求得夹角。（2）连接
，连接
和
交于点
，连接
，易得
，所以为
的中位线，所以
为
中点，所以
的值为1。
（1）取中点，连接
因为
为矩形，
分别为
中点，所以
所以异面直线
与
所成角就是与所成的锐角或直角
因为平面
平面
，平面
平面
矩形中，
，
平面
所以
平面
又
平面，所以
中，
，所以
又
是圆周上点，且
，所以
中，
，由余弦定理可求得
所以异面直线与所成角的余弦值为
（2）连接，连接和交于点，连接
因为直线
平面
，直线
平面
，平面
平面
所以
矩形的对角线交点为中点
所以为的中位线，所以为中点
又
，所以的值为1
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
