题目内容
【题目】在平面直角坐标系xOy中,直线l经过点A(﹣1,0),其倾斜角是α,以原点O为极点,以x轴的非负半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系.设曲线C的极坐标方程是ρ2=6ρcosθ﹣5.
(Ⅰ)若直线l和曲线C有公共点,求倾斜角α的取值范围;
(Ⅱ)设B(x,y)为曲线C任意一点,求 ![]() 的取值范围.
的取值范围.
【答案】解:(Ⅰ)曲线C的极坐标方程转化成直角坐标方程是C:x2+y2﹣6x+5=0,
由题意知直线l的斜率存在,设直线l:y=k(x+1),其中k=tanα.
联立 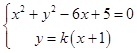
消去y得(1+k2)x2+2(k2﹣3)x+k2+5=0.
因为直线l和曲线C有交点,所以△=4(k2﹣3)2﹣4(1+k2)(k2+5)≥0,
即 ![]() ,
,
即 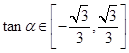 ,
,
所以 ![]() .
.
(Ⅱ)曲线C:x2+y2﹣6x+5=0即(x﹣3)2+y2=4的参数方程是 ![]() (θ为参数),
(θ为参数),
所以点B(x,y)的坐标可以写成(3+2cosθ,2sinθ),
所以 ![]() ,
,
因为sin(θ+ ![]() )∈[﹣1,1],
)∈[﹣1,1],
所以 ![]() x+y∈[3
x+y∈[3 ![]() ﹣4,3
﹣4,3 ![]() +4]
+4]
【解析】(Ⅰ)由x=ρcosθ,y=ρsinθ,代入曲线C的极坐标方程,可得曲线的直角坐标方程,联立直线l的方程,消去y,运用判别式大于等于0,可得斜率的范围,再由斜率公式,可得倾斜角的范围;(Ⅱ)求得曲线C的参数方程,运用两角和的正弦公式和正弦函数的值域,即可得到所求范围.

【题目】某研究型学习小组调查研究高中生使用智能手机对学习的影响,部分统计数据如下:
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 |
|
| |
学习成绩不优秀 |
|
| |
合计 |
(1)根据以上统计数据,你是否有![]() 的把握认为使用智能手机对学习有影响?
的把握认为使用智能手机对学习有影响?
(2)为进一步了解学生对智能手机的使用习惯,现从全校使用智能手机的高中生中(人数很多)随机抽取 ![]() 人,求抽取的学生中学习成绩优秀的与不优秀的都有的概率.
人,求抽取的学生中学习成绩优秀的与不优秀的都有的概率.
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]()