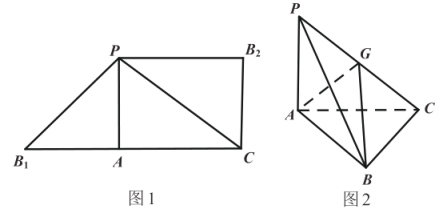
��Ŀ����
����Ŀ����ͼ�����壺����Բ����ΪԲ�ģ�����Ϊֱ����Բ������Բ��������Բ��.����Բ����������һ��M��x��Ĵ��߽���������Բ���ڵ�N������N�ڵ�M���·�ʱ���Ƶ�NΪ��M�����¸�������.��֪��ԲE��![]() �ϵĵ�
�ϵĵ�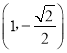 ���¸�����Ϊ��1����1��.
���¸�����Ϊ��1����1��.
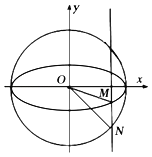
��1������ԲE�ķ��̣�
��2������OMN���������![]() �����¸�����N�����ꣻ
�����¸�����N�����ꣻ
��3����ֱ֪��l��x��my��t��0����ԲE���ڲ�ͬ��A��B���㣬����ԲE�ϴ��ڵ�P������![]() ����ֱ��l��������Χ�ɵ��������������Сֵ.
����ֱ��l��������Χ�ɵ��������������Сֵ.
���𰸡���1��![]() ����2��
����2��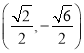 ��
��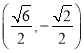 ����3��
����3��![]()
��������
��1��ֱ�Ӹ��ݶ��������a�������õ�b���ɣ�
��2�����N��x0��y0����y0��1�������M��x0��y1����y1��0����������Բ�����Լ�����ɵ�x0y1![]() ��������
��������![]() �����õ�N���ꣻ
�����õ�N���ꣻ
��3����A��x1��y1����B��x2��y2��������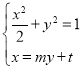 �����Τ�ﶨ����
�����Τ�ﶨ���� ����Ϊ
����Ϊ![]() ��P����Բ�Ͽɵ�4t2��m2+2����ʾ�������������ϻ�������ʽ����������Сֵ.
��P����Բ�Ͽɵ�4t2��m2+2����ʾ�������������ϻ�������ʽ����������Сֵ.
�⣺��1������Բ![]() �ϵĵ㣨1��
�ϵĵ㣨1��![]() �����¸�����Ϊ��1����1����
�����¸�����Ϊ��1����1����
�ศ��Բ�İ뾶ΪR![]() ����Բ������Ϊa��R
����Բ������Ϊa��R![]() ��
��
���㣨1��![]() ��������Բ����
��������Բ����![]() �У����b��1��
�����b��1��
����ԲE�ķ���Ϊ![]() ��
��
��2�����N��x0��y0����y0��1�������M��x0��y1����y1��0��������������ֱ���븨��Բ���̺���Բ���̿ɵã�
x02+y02��2��![]() ����y02��2y12����y0
����y02��2y12����y0![]() y1��
y1��
��S��OMN![]() x0��y1��y0��
x0��y1��y0��![]() ����x0y1
����x0y1![]() ��
��
��x0y1![]() ��
��![]() �����ɽ��
�����ɽ��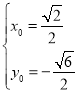 ��
��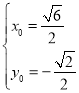 ��
��
���¸�����N������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��3�����������A��x1��y1����B��x2��y2��.
����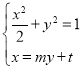 �����ã�m2+2��y2+2mty+t2��2��0�������8��m2+2��t2����0.
�����ã�m2+2��y2+2mty+t2��2��0�������8��m2+2��t2����0.
����Τ�ﶨ���� ��
��
��Ϊ![]() .
.
����![]() ��
��![]()
��Ϊ��P����ԲE�ϣ�
����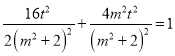 ��
��
������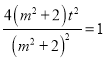 ��
��
��4t2��m2+2��
��ֱ��l��x��my��t��0�У�
����ֱ��l��������Χ�������Σ���t��0��m��0.
��x��0����![]() ����y��0����x��t.
����y��0����x��t.
�������������Ϊ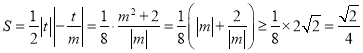 ,
,
���ҽ���m2��2��t2��1ʱ��ȡ�Ⱥţ���ʱ����24��0.
����ֱ��l��������Χ�ɵ��������������СֵΪ![]() .
.