题目内容
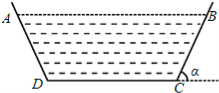
【题目】某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<![]() )为多大时,水渠中水的流失量最小?
)为多大时,水渠中水的流失量最小?
【答案】![]() 时,水渠中水的流失量最小。
时,水渠中水的流失量最小。
【解析】
试题分析:本题考查三角函数在实际问题中的应用,根据题中条件分析,若要减少水的流失量,应使水与渠壁的接触面最小,即求AD+DC+CB的最小值,过B作BE⊥DC,交DC于点E,在![]() 中,
中,![]() ,
,![]() ,由图可知:
,由图可知:![]() ,又因为
,又因为![]() ,所以
,所以![]() ,因此可以求得
,因此可以求得![]() ,于是得到
,于是得到![]() ,整理可以得到:
,整理可以得到:![]() ,由于
,由于![]() 是自变量,S,h是已知量,所以要使函数值y最小,只需使
是自变量,S,h是已知量,所以要使函数值y最小,只需使![]() 的值最小即可。设
的值最小即可。设![]() ,u可看作(0,2)与(﹣sinα,cosα)两点连线的斜率,由于α∈(0,
,u可看作(0,2)与(﹣sinα,cosα)两点连线的斜率,由于α∈(0,![]() ),
),
点(﹣sinα,cosα)在曲线x2+y2=1(﹣1<x<0,0<y<1)上运动,当过(0,2)的直线与曲线相切时,直线斜率最小,此时切点为(﹣![]() ,
,![]() ),则有sinα=
),则有sinα=![]() ,且cosα=
,且cosα=![]() ,故当α=
,故当α=![]() 时,水渠中水的流失量最小.
时,水渠中水的流失量最小.
试题解析:作BE⊥DC于E,
在Rt△BEC中,BC=![]() ,CE=hcotα,
,CE=hcotα,
又AB﹣CD=2CE=2hcotα,AB+CD=![]() ,
,
故CD=![]() ﹣hcotα.
﹣hcotα.
设y=AD+DC+BC,
则y=![]() ﹣hcotα+
﹣hcotα+![]() =
=![]() +
+![]() (0<α<
(0<α<![]() ),
),
由于S与h是常量,欲使y最小,只需u=![]() 取最小值,
取最小值,
u可看作(0,2)与(﹣sinα,cosα)两点连线的斜率,
由于α∈(0,![]() ),
),
点(﹣sinα,cosα)在曲线x2+y2=1
(﹣1<x<0,0<y<1)上运动,
当过(0,2)的直线与曲线相切时,直线斜率最小,
此时切点为(﹣![]() ,
,![]() ),
),
则有sinα=![]() ,且cosα=
,且cosα=![]() ,
,
那么α=![]() ,
,
故当α=![]() 时,水渠中水的流失量最小.
时,水渠中水的流失量最小.



 名校课堂系列答案
名校课堂系列答案


