题目内容
【题目】设函数![]() 若函数
若函数![]() 的图象与
的图象与![]() 轴相邻两个交点间的距离为
轴相邻两个交点间的距离为![]() ,且图像的一条对称轴是直线
,且图像的一条对称轴是直线![]() 。
。
(1)求![]() 的值;
的值;
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)画出函数![]() 在区间
在区间![]() 上的图像。
上的图像。
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】
试题分析:(1)由图象与x轴的任意两个相邻交点间的距离为![]() ,可得出函数的周期,再由对称轴是直线
,可得出函数的周期,再由对称轴是直线![]() 可求出
可求出![]() 值;
值;
(2)由(1)的出的函数解析式![]() ,可运用正弦函数的单调性,解不等式可求函数的单调增区间;
,可运用正弦函数的单调性,解不等式可求函数的单调增区间;
(3)由函数解析式![]() ,可运用“五点”作图法,注意所要求的区间
,可运用“五点”作图法,注意所要求的区间![]() ,
,
可通过列表(关键点),描点,连线得出函数图像。
试题解析:(1)函数![]() 的图象与
的图象与![]() 轴的两个相邻交点间的距离为
轴的两个相邻交点间的距离为![]() ,
,
![]() ,又函数图像的一条对称轴是直线
,又函数图像的一条对称轴是直线![]()
![]()
![]()
![]()
(2)由(1)可知![]()
![]() 得:
得:![]()
所以函数![]() 的单调增区间是
的单调增区间是![]() ;
;
(3)
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
、
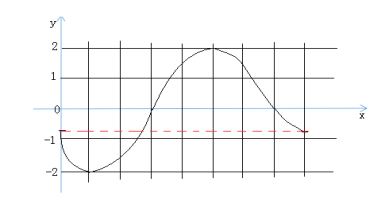
所以函数![]() 在区间
在区间![]() 上的图像为:
上的图像为:

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切正整数
,对一切正整数![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上,记
的图象上,记![]() 与
与![]() 的等差中项为
的等差中项为![]() 。
。
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)设集合![]() ,等差数列
,等差数列![]() 的任意一项
的任意一项![]() ,其中
,其中![]() 是
是![]() 中的最小数,且
中的最小数,且![]() ,求
,求![]() 的通项公式。
的通项公式。
【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间的关系,下表记录了小李某月连续5天每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的关系:
之间的关系:
时间 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
(Ⅰ)请根据上表提供的数据,用最小二乘法求出投篮命中率![]() 与打篮球时间
与打篮球时间![]() (单位:小时)之间的回归直线方程
(单位:小时)之间的回归直线方程![]() ;
;
(Ⅱ)如果小李某天打了2.5小时篮球,预测小李当天的投篮命中率.
(参考:用最小二乘法求线性回归方程系数公式 ,
,![]() )
)
【题目】从某大学一年级女生中,选取身高分别是150cm、155cm、160cm、165cm、170cm的学生各一名,其身高和体重数据如表所示:
身高/cm ( | 150 | 155 | 160 | 165 | 170 |
体重/kg ( | 43 | 46 | 49 | 51 | 56 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,计算身高为168cm时,体重的估计值![]() 为多少?
为多少?
参考公式:线性回归方程![]() ,其中
,其中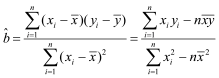 ,
,![]() .
.