题目内容
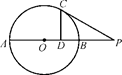
如图,PA切圆O于点A,割线PBC交圆O于点B、C,∠APC的角平分线分别与AB、AC相交于点D、E,求证:
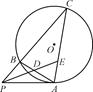
(1)AD=AE;
(2)AD2=DB·EC.

(1)AD=AE;
(2)AD2=DB·EC.
(1)见解析(2)见解析
证明:(1)∠AED=∠EPC+∠C,∠ADE=∠APD+∠PAB.因为PE是∠APC的角平分线,所以∠EPC=∠APD.又PA是圆O的切线,故∠C=∠PAB.所以∠AED=∠ADE.所以AD=AE.
(2) ,△PCE∽△PAD,
,△PCE∽△PAD,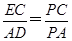 .
.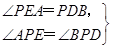 ,△PAE∽△PBD,
,△PAE∽△PBD,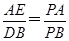 .又PA是切线,PBC是割线
.又PA是切线,PBC是割线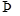 PA2=PB·PC?
PA2=PB·PC? .故
.故 .又AD=AE,所以AD2=DB·EC.
.又AD=AE,所以AD2=DB·EC.
(2)
 ,△PCE∽△PAD,
,△PCE∽△PAD,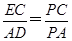 .
.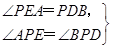 ,△PAE∽△PBD,
,△PAE∽△PBD,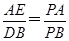 .又PA是切线,PBC是割线
.又PA是切线,PBC是割线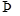 PA2=PB·PC?
PA2=PB·PC? .故
.故 .又AD=AE,所以AD2=DB·EC.
.又AD=AE,所以AD2=DB·EC.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
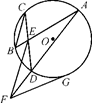

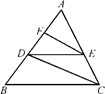
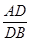 =2,那么△ADE与四边形DBCE的面积比是( )
=2,那么△ADE与四边形DBCE的面积比是( )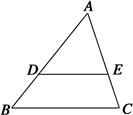
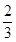 B.
B.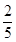 C.
C.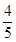 D.
D.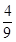
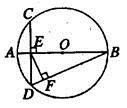
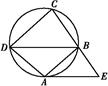
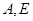 是半圆周上的两个三等分点,直径
是半圆周上的两个三等分点,直径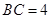 ,
,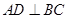 ,垂足为D,
,垂足为D, 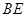 与
与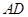 相交与点F,则
相交与点F,则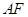 的长为 。
的长为 。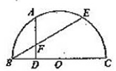
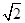 ,求AF的长.
,求AF的长.