题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间及极值;
的单调区间及极值;
(2)当![]() 时,求证:
时,求证:![]() .
.
【答案】(1)![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;
;![]() ,没有极小值;(2)证明见解析.
,没有极小值;(2)证明见解析.
【解析】
(1)求函数的导数,利用导数求函数的单调区间、极值即可(2)构造函数![]() ,利用导数,分类讨论求函数
,利用导数,分类讨论求函数![]() 的最小值,转化为最小值不小于0即可,也可构造函数后变换主元为
的最小值,转化为最小值不小于0即可,也可构造函数后变换主元为![]() 求其最大值也可证明.
求其最大值也可证明.
(1)当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减
上单调递减
由![]() 得:
得:![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 函数
函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
![]() ,但
,但![]() 没有极小值.
没有极小值.
(2)证明:
证法一
令![]()
![]()
①当![]() 时,
时,![]() ,故
,故![]()
②当![]() 时,
时,![]() 在
在![]() 上是增函数
上是增函数
由![]() 得:
得:![]()
![]() 当
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减
上单调递减
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增
上单调递增
![]()
![]()
![]()
![]()
由![]() 知:
知:![]()
![]() ,于是
,于是![]()
![]() ,即
,即![]()
综上所述,当![]() 时,
时,![]() .
.
证法二
![]() 即
即![]() ,其中
,其中![]() ,
,![]()
以![]() 为主元,设
为主元,设![]() ,
,![]() ,则
,则
当![]() 时,
时,![]()
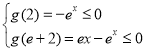 .
.
由![]() 知
知![]() 对任意
对任意![]() 成立.
成立.
令![]() ,则
,则![]() 在
在![]() 上单调递减
上单调递减
又![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]()
![]() 对任意
对任意![]() ,都有
,都有![]() ,即
,即![]()
综上所述,当![]() 时,
时,![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】“绿水青山就是金山银山”,“建设美丽中国”已成为新时代中国特色社会主义生态文明建设的重要内容,某班在一次研学旅行活动中,为了解某苗圃基地的柏树幼苗生长情况,在这些树苗中随机抽取了120株测量高度(单位:![]() ),经统计,树苗的高度均在区间
),经统计,树苗的高度均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图.据当地柏树苗生长规律,高度不低于
分成6组,制成如图所示的频率分布直方图.据当地柏树苗生长规律,高度不低于![]() 的为优质树苗.
的为优质树苗.
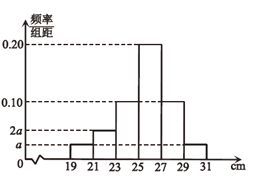
(1)求图中![]() 的值;
的值;
(2)已知所抽取的这120株树苗来自于![]() ,
,![]() 两个试验区,部分数据如列联表:
两个试验区,部分数据如列联表:
|
| 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整,并判断是否有99.9%的把握认为优质树苗与![]() ,
,![]() 两个试验区有关系,并说明理由;
两个试验区有关系,并说明理由;
(3)用样本估计总体,若从这批树苗中随机抽取4株,其中优质树苗的株数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
附:参考公式与参考数据: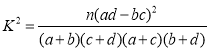 ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
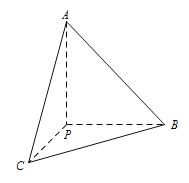
【题目】如图,在直角梯形![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为折痕把
为折痕把![]() 折起,当几何体
折起,当几何体![]() 的的体积最大时,则下列命题中正确的个数是( )
的的体积最大时,则下列命题中正确的个数是( )

①![]()
②![]() ∥平面
∥平面![]()
③![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角
所成的角
④![]() 与
与![]() 所成的角等于
所成的角等于![]() 与
与![]() 所成的角
所成的角
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】《厉害了,我的国》是2018年在我国各影院上映的一部非常火的电影纪录片,该部影片主要讲述了我国近几年的发展现状和成就,影片通过讲述中国故事,刻画中国面貌,弘扬了中国精神,引起了国民的高度关注,上映仅半个月影片票房就突破了3亿元,刷新了我国纪录片的票房纪录,某市一电影院为了解该影院观看《厉害了,我的国》的观众的年龄构成情况,随机抽取了40名观众数据统计如表:
年龄/岁 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) |
人数 | 6 | 8 | 12 | 6 | 4 | 2 | 2 |
(1)求所调查的40名观众年龄的平均数和中位数;
(2)该电影院决定采用抽奖方式来提升观影人数,将《厉害了,我的国》的电影票票价提高20元/张,并允许购买电影票的观众抽奖3次,中奖1次、2次、3次分别奖现金20元、30元、60元,设观众每次中奖的概率均为![]() ,则观众在3次抽奖中所获得的奖金总额的数学期望是多少元(结果保留整数)?
,则观众在3次抽奖中所获得的奖金总额的数学期望是多少元(结果保留整数)?