题目内容
【题目】在三棱锥P﹣ABC中,已知PA,PB,PC两两垂直,PB=3,PC=4,且三棱锥P﹣ABC的体积为10.
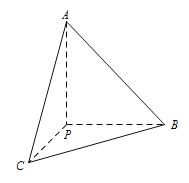
(1)求点A到直线BC的距离;
(2)若D是棱BC的中点,求异面直线PB,AD所成角的大小(结果用反三角函数值表示).
【答案】(1)![]() (2)arccos
(2)arccos![]()
【解析】
(1)先根据已知的体积和棱长求出![]() ,结合直角三角形的知识可求点A到直线BC的距离;
,结合直角三角形的知识可求点A到直线BC的距离;
(2)建立空间直角坐标系,写出向量![]() 的坐标,利用向量夹角公式可求.
的坐标,利用向量夹角公式可求.
(1)在三棱锥P﹣ABC中,PA,PB,PC两两垂直,
∵PB=3,PC=4,且三棱锥P﹣ABC的体积为10.
∴VP﹣ABC=VA﹣PBC![]() 10,解得PA=5,
10,解得PA=5,
过P作PO⊥BC,交BC于O,连结PO,如图,
由三垂线定理得AO⊥BC,
∵![]() ,∴PO
,∴PO![]() ,
,
∴点A到直线BC的距离:
AO![]() .
.
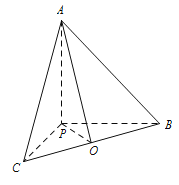
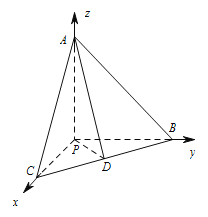
(2)以P为原点,PC,PB,PA所在直线分别为x轴, y轴, z轴,建立空间直角坐标系,
则A(0,0,5),P(0,0,0),B(0,3,0),C(4,0,0),D(2,![]() ,0),
,0),
![]() (0,3,0),
(0,3,0),![]() (2,
(2,![]() ,﹣5),
,﹣5),
设异面直线PB,AD所成角的大小为θ,
则cosθ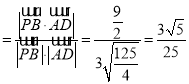 .
.
∴异面直线PB,AD所成角的大小为arccos![]() .
.

【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
【题目】某房产中介统计了深圳市某高档小区从2018年12月至2019年11月当月在售二手房均价(单位:万元/平方米)的散点图,如下图所示,图中月份代码1至12分别对应2018年12月至2019年11月的相应月份.
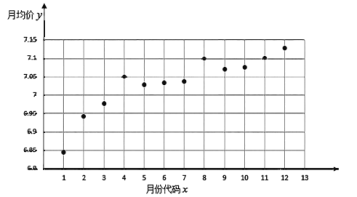
根据散点图选择![]() 和
和![]() 两个模型进行拟合,根据数据处理得到两个回归方程分别为
两个模型进行拟合,根据数据处理得到两个回归方程分别为![]() 和
和![]() ,并得到以下一些统计量的值:
,并得到以下一些统计量的值:
|
| |
残差平方和 | 0.0148557 | 0.0048781 |
总偏差平方和 | 0.069193 | |
(1)请利用相关指数![]() 判断哪个模型的拟合效果更好;
判断哪个模型的拟合效果更好;
(2)某位购房者拟于2020年5月份购买深圳市福田区![]() 平方米的二手房(欲购房为其家庭首套房).若该小区所有住房的房产证均已满3年,请你利用(1)中拟合效果更好的模型解决以下问题:
平方米的二手房(欲购房为其家庭首套房).若该小区所有住房的房产证均已满3年,请你利用(1)中拟合效果更好的模型解决以下问题:
(i)估算该购房者应支付的购房金额.(购房金额=房款+税费;房屋均价精确到0.01万元/平方米)
(ii)若该购房者拟用不超过760万元的资金购买该小区一套二手房,试估算其可购买的最大面积(精确到1平方米)
附注:根据有关规定,二手房交易需要缴纳若干项税费,税费是按照房屋的计税价格进行征收.(计税价格=房款)
征收方式见下表:
购买首套房面积 |
|
|
|
契税(买方缴纳)的税率 |
|
|
|
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式:相关指数 .
.
