Question

【题目】“绿水青山就是金山银山”，“建设美丽中国”已成为新时代中国特色社会主义生态文明建设的重要内容，某班在一次研学旅行活动中，为了解某苗圃基地的柏树幼苗生长情况，在这些树苗中随机抽取了120株测量高度（单位：），经统计，树苗的高度均在区间内，将其按，，，，，分成6组，制成如图所示的频率分布直方图.据当地柏树苗生长规律，高度不低于的为优质树苗.

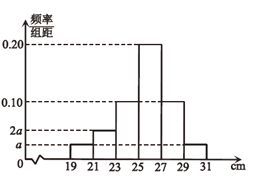
（1）求图中的值；

（2）已知所抽取的这120株树苗来自于，两个试验区，部分数据如列联表：

	试验区	试验区	合计
优质树苗		20
非优质树苗	60
合计

将列联表补充完整，并判断是否有99.9%的把握认为优质树苗与，两个试验区有关系，并说明理由；

（3）用样本估计总体，若从这批树苗中随机抽取4株，其中优质树苗的株数为，求的分布列和数学期望.

附：参考公式与参考数据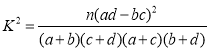：，其中

	0.010	0.005	0.001
	6.635	7.879	10.828

Answer 1

【答案】（1）；（2）列联表见解析，没有99.9%的把握认为优质树苗与两个试验区有关系；（3）分布列见解析，

【解析】

（1）由频率分布直方图中所有频率（小矩形面积）和为1可求得；

（2）由频率分布直方图求出优质树苗和非优质树苗的株数后可填写列联表，求出后知有无关系；

（3）由（2）知这批树苗为优质树苗的概率为，的可能取值为0，1，2，3，4， 服从二项分布，即，计算出各概率，得分布列，根据期望公式计算出期望．

（1）根据频率分布直方图数据，有，解得：.

（2）根据频率分布直方图可知，样本中优质树苗棵树有

列联表如下：

	试验区	试验区	合计
优质树苗	10	20	30
非优质树苗	60	30	90
合计	70	50	120

可得；

所以，没有99.9%的把握认为优质树苗与两个试验区有关系

注：也可由得出结论

（3）用样本估计总体，由题意，这批树苗为优质树苗的概率为

的可能取值为0，1，2，3，4，由题意知：服从二项分布，即

即：；；

；；

.

的分布列为：

	0	1	2	3

数学期望为

（或）.