Question

【题目】已知椭圆：过点，且椭圆的离心率为．

(Ⅰ)求椭圆的方程；

(Ⅱ)斜率为的直线交椭圆于，两点，且．若直线上存在点P，使得是以为顶角的等腰直角三角形，求直线的方程．

Answer 1

【答案】(Ⅰ) (Ⅱ) y=x-1

【解析】

（Ⅰ）由椭圆C：1（a＞b＞0）过点A（0，1），且椭圆的离心率为，列方程组求出a，b，由此能求出椭圆C的方程．

（Ⅱ）设直线l的方程为y＝x+m，P（3，yP），由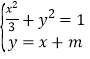，得4x2+6mx+3m2﹣3＝0，利用根的判别式、韦达定理、中点坐标公式，结合已知条件能求出直线l的方程．

（Ⅰ）由题意得

解得．

所以椭圆的方程为．

（Ⅱ）设直线l的方程为y=x+m，

由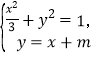得.

令，得．

，．

因为是以为顶角的等腰直角三角形，

所以平行于轴．

过做的垂线，则垂足为线段的中点．

设点的坐标为，则．

由方程组解得，即．

而，

所以直线的方程为y=x-1．