题目内容
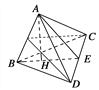
【题目】 如图,在三棱锥A-BCD中,CA=CB,DA=DB.作BE⊥CD,E为垂足,作AH⊥BE于H.求证:AH⊥平面BCD.

【答案】详见解析
【解析】
试题证明线面垂直,可利用线面垂直的判定定理,证明直线与平面内的两条相交直线垂直,进而说明线面垂直.本题利用两个等腰三角形三线合一,取AB的中点F,连接DF、CF,得出线面垂直,从而证明AB与CD垂直,又利用CD与BE垂直,从而得出线CD与面ABE垂直,得出CD与AH垂直,又AH与BE垂直,于是证明出线面垂直.
试题解析:
取AB的中点F,连接CF、DF.
∵CA=CB,DA=DB,∴CF⊥AB,DF⊥AB.
∵CF∩DF=F,∴AB⊥平面CDF.
∵CD平面CDF,∴AB⊥CD.
又CD⊥BE,AB∩BE=B,∴CD⊥平面ABE.
∵AH平面ABE,∴CD⊥AH.
∵AH⊥BE,BE∩CD=E,∴AH⊥平面BCD.

练习册系列答案
相关题目