题目内容
11．下列说法正确的是（ ）| A． | 对于任意的x都有|x|≤2x恒成立 | |
| B． | 同时向上抛掷2枚硬币，2枚都是反面朝上的概率是$\frac{1}{4}$ | |
| C． | 回归直线必须过（0，0）并呈现一条直线 | |
| D． | 在k班高三数学期中测试中，平均数能够代表K班数学总体水平 |
分析 举出反例x＜0，可判断A；求出满足条件的事件的概率，可判断B；根据回归直线的几何特征，可判断C；根据平均数表示刻画数据总体水平的适用范围，可判断D．
解答 解：当x＜0时，|x|＞2x，故A错误；
同时向上抛掷2枚硬币，2枚都是反面朝上的概率是$\frac{1}{4}$，故B正确；
回归直线必须过（$\overline{x}$，$\overline{y}$）并呈现一条直线，但不一定经过（0，0）点，故C错误；
如果数学成绩差距较大，则平均数不能够代表K班数学总体水平，故D错误，
故选：B
点评 本题考查的知识点是命题的真假判断与应用，此类题型往往综合较多的其它知识点，综合性强，难度中档．
练习册系列答案
相关题目
2．
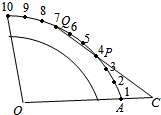某转弯路段为四分之一圆环，圆环道路外侧均匀栽种了10棵树（如图所示），小李在半径OA的延长线上一点C处观察到第四棵树（P点），第七棵树（Q点）与点C在同一条直线上，并测得AC=100米，则此弧形道路的大圆半径OA的长为（ ）
某转弯路段为四分之一圆环，圆环道路外侧均匀栽种了10棵树（如图所示），小李在半径OA的延长线上一点C处观察到第四棵树（P点），第七棵树（Q点）与点C在同一条直线上，并测得AC=100米，则此弧形道路的大圆半径OA的长为（ ）| A． | 100$\sqrt{3}$米 | B． | 100（$\sqrt{3}$+1）米 | C． | 200米 | D． | 100（$\sqrt{3}$+$\sqrt{2}$）米 |
19．已知命题p：?x0∈R，${9}^{{x}_{0}}$-m•${3}^{{x}_{0}}$+4≤0，若p为真命题，则实数m的取值范围是（ ）
| A． | （4，+∞） | B． | [4，+∞） | C． | （-∞，4） | D． | （-∞，4] |