题目内容
6.设函数f(x)=x|x-a|+a,(a≥0).(1)若a=1,求函数f(x)的零点;
(2)若x∈[-1,1]时,|f(x)|≤1恒成立,求实数a的最大值.|
分析 (1)化简函数f(x)的解析式,再令f(x)=0,求得x的值,即为所求.
(2)作出函数f(x)的图象,利用二次函数的性质、数形结合、分类讨论求得a的范围,可得实数a的最大值.
解答 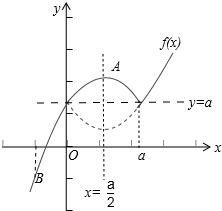 解:(1)若a=1,函数f(x)=x|x-a|+a=x|x-1|+1=$\left\{\begin{array}{l}{x(x-1)+1,x≥1}\\{x(1-x)+1,x<1}\end{array}\right.$,
解:(1)若a=1,函数f(x)=x|x-a|+a=x|x-1|+1=$\left\{\begin{array}{l}{x(x-1)+1,x≥1}\\{x(1-x)+1,x<1}\end{array}\right.$,
令f(x)=0,求得x=$\frac{1-\sqrt{5}}{2}$,故函数f(x)的零点为$\frac{1-\sqrt{5}}{2}$.
(2)若x∈[-1,1]时,|f(x)|≤1恒成立,则-1≤f(x)≤1.
又 f(x)=x|x-a|+a=$\left\{\begin{array}{l}{{x}^{2}-ax+a,x≥a}\\{{-x}^{2}+ax+a,x<a}\end{array}\right.$,(a≥0),如图所示:
①当$\frac{a}{2}$≤1,即0≤a≤2时,在[-1,1]上,f(x)的最大值为f($\frac{a}{2}$)=a+$\frac{1}{4}$a2,最小值f(-1)=-1,
由题意可得$\left\{\begin{array}{l}{0≤a≤2}\\{|f(\frac{a}{2})|=|a-\frac{{a}^{2}}{4}|≤1}\\{|f(-1)=|-1|≤1}\end{array}\right.$,求得 0≤a≤2.
②当$\frac{a}{2}$≥1,即a≥2时,在[-1,1]上,f(x)的最大值为f(1)=-1+2a,最小值f(-1)=-1,
由题意可得$\left\{\begin{array}{l}{a>2}\\{|f(1)|=|-1+2a|≤1}\\{|f(-1)|=|-1|≤1}\end{array}\right.$,求得a∈∅.
综上可得,a的最大值为2.
点评 本题主要考查带有绝对值的函数,函数的零点的求法,函数的恒成立问题,体现了转化、分类讨论的数学思想,属于中档题.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | 对于任意的x都有|x|≤2x恒成立 | |
| B. | 同时向上抛掷2枚硬币,2枚都是反面朝上的概率是$\frac{1}{4}$ | |
| C. | 回归直线必须过(0,0)并呈现一条直线 | |
| D. | 在k班高三数学期中测试中,平均数能够代表K班数学总体水平 |