题目内容
7.已知A是曲线ρ=4cosθ上任一点,则点A到直线ρcosθ=-1距离的最大值为5.分析 把极坐标化为直角坐标方程,求出圆心到直线的距离d,即可得出点A到直线ρcosθ=-1距离的最大值为d+r.
解答 解:曲线ρ=4cosθ化为ρ2=4ρcosθ,∴x2+y2=4x,∴(x-2)2+y2=4,
直线ρcosθ=-1化为x=-1.
∴圆心(2,0)到直线x=-1的距离d=3,
∴点A到直线ρcosθ=-1距离的最大值为d+r=3+2=5.
故答案为:5.
点评 本题把极坐标化为直角坐标方程、点到直线的距离公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
2.在如图所示的四个图示中,是结构图的是( )
| A. | 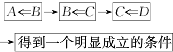 | B. | 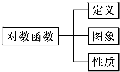 | ||
| C. | 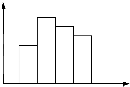 | D. |  |
12.把函数y=sin(2x+$\frac{π}{6}$)的图象向右平移$\frac{π}{6}$个单位得到函数f(x)的图象,则下列说法正确的是( )
| A. | f(x)的图象关于y轴对称 | B. | f(x)的图象关于原点对称 | ||
| C. | f(x)的图象关于直线x=$\frac{π}{3}$对称 | D. | f(x)的图象关于点($\frac{π}{3}$,0)对称 |
17.若实数a,b满足a2+b2≤1,则关于x的方程x2-ax+$\frac{3}{4}$b2=0有实数根的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | 1 |