题目内容
下列说法错误的是 ( )
| A.命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” |
| B.“x>1”是“|x|>1”的充分不必要条件 |
| C.若p且q为假命题,则p、q均为假命题 |
| D.命题p:“?x∈R,使得x2+x+1<0”,则¬p:“?x∈R,均有x2+x+1≥0” |
C
解析试题分析:A.命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”
对,逆否命题知识将原命题条件与结论交换并加以否定;
B.“x>1”是“|x|>1”的充分不必要条件,对,由x>1可得|x|>1,但由|x|>1得到的是x>1或x<-1;
C.若p且q为假命题,则p、q均为假命题,不对,因为,p且q为假命题时 ,p,q有一为假命题,其即为假命题;
D.命题p:“?x∈R,使得x2+x+1<0”,则¬p:“?x∈R,均有x2+x+1≥0”对,因为存在性命题的否定是全称命题。故选C
考点:本题主要考查命题的概念,充要条件的概念。
点评:基础题,充要条件的判断问题,是高考不可少的内容,特别是充要条件可以和任何知识点相结合。充要条件的判断一般有三种思路:定义法、等价关系转化法、集合关系法。存在性命题的否定是全称命题。

练习册系列答案
相关题目
设α、β是两个不同的平面,l、m为两条不同的直线,命题p:若α∥β,l?α,m?β则l∥m;命题q:l∥α,m⊥l,m?β,则α⊥β.则下列命题为真命题的是( )
| A.p或q | B.p且q |
| C.非p或q | D.p且非q |
若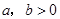 ,则
,则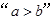 是“
是“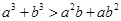 ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充分且必要条件 | D.既非充分也非必要条件 |
下列说法中错误的个数是( )
①一个命题的逆命题为真,它的否命题也一定为真;
②命题“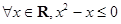 ”的否定是“
”的否定是“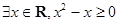 ”;
”;
③“矩形的两条对角线相等”的逆命题是真命题;
④“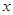 ≠3”是“|
≠3”是“|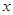 |≠3”成立的充分条件.
|≠3”成立的充分条件.
| A.1 | B.2 | C.3 | D.4 |
在四边形ABCD中,“ ,且
,且 ”是“四边形ABCD是菱形”的
”是“四边形ABCD是菱形”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知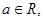 则
则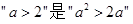 成立的( )
成立的( )
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条件 |
“1≤x≤4”是“1≤x2≤16”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若“ ,
, ”为真命题,则实数
”为真命题,则实数 的取值范围是 ( )
的取值范围是 ( )
A.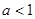 | B. | C. | D. |
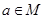 则
则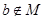 ”的逆否命题是 ( )
”的逆否命题是 ( )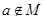 ,则
,则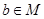 D、若
D、若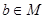 ,则
,则