题目内容
11.函数f(x)=sin2x+4cosx+2的值域为( )| A. | (-∞,3] | B. | [-2,6] | C. | [-2,7] | D. | (-∞,7] |
分析 函数f(x)=-(cosx-2)2+7,结合cosx∈[-1,1],利用二次函数的性质求得它的值域.
解答 解:函数f(x)=sin2x+4cosx+2=-cos2x+4cosx+3=-(cosx-2)2+7,
由于cosx∈[-1,1],故当cosx=1时,f(x)取得最大值为 6,当cosx=-1时,f(x)取得最小值为-2,
故函数f(x)的值域为[-2,6],
故选:B.
点评 本题主要考查同角三角函数的基本关系、二次函数的性质应用,属于基础题.

练习册系列答案
相关题目
14.函数$f(x)=\frac{1}{x-5}{log_2}(x-3)$的定义域是( )
| A. | (-∞,5)∪(5,+∞) | B. | (3,+∞) | C. | (3,5) | D. | (3,5)∪(5,+∞) |
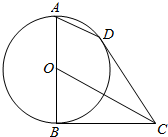 如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.
如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.