题目内容
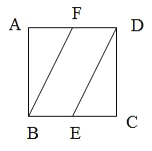
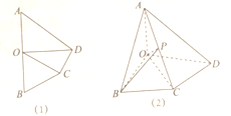
【题目】如图，在矩形
中，
，
，
是
的中点，以
为折痕将
向上折起，
变为
，且平面
平面
.
（Ⅰ）求证：
；
（Ⅱ）求点到平面
的距离
.
【答案】（Ⅰ）见解析;（Ⅱ）
.
【解析】【试题分析】(I)利用勾股定理证得
,根据面面垂直的性质定理可知
平面
,所以
.(II)利用等体积法,通过化简
来求得点
到平面
的距离.
【试题解析】
（Ⅰ）证明：∵
，
，
∴ AB2=AE2+BE2∴ AE⊥EB.
取
的中点
，连结
，则
，
∵ 平面
平面
，
∴
平面，∴ 
，
从而
平面，∴
（Ⅱ）由（Ⅰ）知MD′⊥平面ABCE，且MD′=
，S⊿AEB=4
易知：BM=
，BD′=2
，
而点E到平面ABD′的距离为d，
由VE- ABD′= VD′- ABE得：
2d = 
，
∴d = .
练习册系列答案
相关题目
【题目】从某保险公司的推销员中随机抽取50名，统计这些推销员某月的月销售额（单位：千元），由统计结果得如图频数分别表：
月销售额 分组 | [12.25，14.75） | [14.75，17.25） | [17.25，19.75） | [19.75，22.25） | [22.25，24.75） |
频数 | 4 | 10 | 24 | 8 | 4 |
（1）作出这些数据的频率分布直方图；
（2）估计这些推销员的月销售额的平均数（同一组中的数据用该组区间的中点作代表）；
（3）根据以上抽样调查数据，公司将推销员的月销售指标确定为17.875千元，试判断是否有60%的职工能够完成该销售指标．
