题目内容
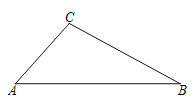
【题目】已知在四棱锥![]() 中,
中, ![]() 为正三角形,
为正三角形, ![]() ,底面
,底面![]() 为平行四边形,平面
为平行四边形,平面![]() 平面
平面![]() ,点
,点![]() 是侧棱
是侧棱![]() 的中点,平面
的中点,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
(1)求证: ![]() ;
;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角(锐角)的余弦值.
所成二面角(锐角)的余弦值.

【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由底面![]() 是平行四边形,利用线面平行的判定定理得
是平行四边形,利用线面平行的判定定理得![]() 面
面![]() ,在利用线面平行的性质定理,即可证得
,在利用线面平行的性质定理,即可证得![]() .
.
(2)建立空间直角坐标系![]() ,求得平面
,求得平面![]() 和平面
和平面![]() 的一个法向量,利用空间向量的夹角公式,即可求解平面
的一个法向量,利用空间向量的夹角公式,即可求解平面![]() 和平面
和平面![]() 的二面角的余弦值.
的二面角的余弦值.
试题解析:
(1)∵底面![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,
又∵![]() 面
面![]() 面
面![]() ,
, ![]() 面
面![]() ,
,
又∵![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ,
,
![]() .
.
(2)取![]() 中点
中点![]() ,连接
,连接![]() 侧面
侧面![]() 为正三角形,故
为正三角形,故![]() ,又
,又![]() 平面
平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() , 在平行四边形
, 在平行四边形![]() 中,
中, ![]() ,故
,故![]() 为菱形, 且
为菱形, 且![]() 是
是![]() 中点,
中点, ![]() .
.
如图,建立空间直角坐标系![]() ,
,
因为![]() ,则
,则![]() ,
,
又![]() ,点
,点![]() 是棱
是棱![]() 中点,
中点, ![]() 点
点![]() 是棱
是棱![]() 中点,
中点,  ,
,
 ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
则有 , 不妨令
, 不妨令![]() ,则平面
,则平面![]() 的一个法向量为
的一个法向量为![]() 平面
平面![]()
![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
 ,
,
∴平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】已知![]() 三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
(Ⅰ)试估计![]() 班学生人数;
班学生人数;
(Ⅱ)从![]() 班和
班和![]() 班抽出来的学生中各选一名,记
班抽出来的学生中各选一名,记![]() 班选出的学生为甲,
班选出的学生为甲,![]() 班选出的学生为乙,若学生锻炼相互独立,求甲的锻炼时间大于乙的锻炼时间的概率.
班选出的学生为乙,若学生锻炼相互独立,求甲的锻炼时间大于乙的锻炼时间的概率.