题目内容
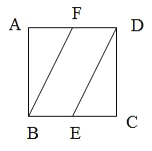
【题目】如图，在棱长为1正方体
中，点
，
分别为边
，
的中点，将
沿
所在的直线进行翻折，将
沿
所在直线进行翻折，在翻折的过程中，下列说法错误的是（ ）
A. 无论旋转到什么位置，
、
两点都不可能重合
B. 存在某个位置，使得直线
与直线
所成的角为
C. 存在某个位置，使得直线与直线所成的角为
D. 存在某个位置，使得直线
与直线
所成的角为
【答案】D
【解析】
利用圆锥的几何特征逐一判断即可.
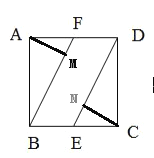
解：过A点作AM⊥BF于M，过C作CN⊥DE于N点
在翻折过程中，AF是以F为顶点，AM为底面半径的圆锥的母线，同理，AB，EC，DC也可以看成圆锥的母线；
在A中，A点轨迹为圆周，C点轨迹为圆周，显然没有公共点，故A正确；
在B中，能否使得直线AF与直线CE所成的角为60°，又AF，EC分别可看成是圆锥的母线，只需看以F为顶点，AM为底面半径的圆锥的轴截面的顶角是否大于等于60°即可，故B正确；
在C中，能否使得直线AF与直线CE所成的角为90°，只需看以F为顶点，AM为底面半径的圆锥的轴截面的顶角是否大于等于90°即可，故C正确；
在D中，能否使得直线
与直线
所成的角为
，只需看以B为顶点，AM为底面半径的圆锥的轴截面的顶角是否大于等于90°即可，故D不成立；
故选：D．
练习册系列答案
相关题目
