题目内容
6.在函数①y=sin|2x|,②y=1-$2{sin^2}(x-\frac{π}{6})$,③$y=\frac{{tan\frac{x}{2}}}{{1-{{tan}^2}\frac{x}{2}}}$,④$y=tan(x-\frac{π}{3})$中,最小正周期为π的所有函数为( )| A. | ①② | B. | ②③④ | C. | ②③ | D. | ③④ |
分析 逐一求出各个函数的最小正周期,从而得出结论.
解答 解:∵函数①y=sin|2x|不是周期函数,没有最小正周期,不满足条件;
②y=1-$2{sin^2}(x-\frac{π}{6})$=cos(2x-$\frac{π}{3}$)的最小正周期为$\frac{2π}{2}$=π,满足条件;
③$y=\frac{{tan\frac{x}{2}}}{{1-{{tan}^2}\frac{x}{2}}}$=$\frac{1}{2}$tanx的最小正周期为π,满足条件;
④$y=tan(x-\frac{π}{3})$的最小正周期为$\frac{π}{1}$=π,满足条件,
故②③④都满足条件,
故选:B.
点评 本题主要考查二倍角公式,三角函数的周期性及其求法,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
17.已知{an}是等差数列,Sn为其前n项和,若S13=S2000,则S2013=( )
| A. | -2014 | B. | 2014 | C. | 1007 | D. | 0 |
14.等差数列{an}的前n项和为Sn,已知(a1006-1)3+2014(a1006-1)=1,(a1009-1)3+2014(a1009-1)=-1,则( )
| A. | S2014=2014,a1009>a1006 | B. | S2014=2014,a1009<a1006 | ||
| C. | S2014=-2014,a1009>a1006 | D. | S2014=-2014,a1009<a1006 |
1.函数y=$\sqrt{1-(\frac{1}{2})^{x}}$的值域为( )
| A. | [0,+∞) | B. | (0,1) | C. | [0,1) | D. | [0,1] |
15.能够把圆O:x2+y2=16的周长和面积同时分成相等的两部分的函数称为圆O的“和谐函数”,下列函数不是圆O的“和谐函数”的是( )
| A. | f(x)=ln[(4-x)(4+x)] | B. | f(x)=tan$\frac{x}{2}$ | C. | f(x)=ex-e-x | D. | f(x)=x3 |
16.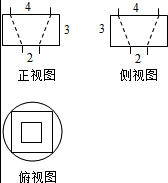 若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( )
若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( )
 若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( )
若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( )| A. | (18π-20)cm2cm3 | B. | (24π-20)cm3 | C. | (18π-28)cm23 | D. | (24π-28)cm3 |