题目内容
14.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点点分别为F1,F2,点P是C上的点,PF1⊥F1F2,∠PF2F1=45°,则C的离心率为( )| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}-1$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 利用PF1⊥F1F2,∠PF2F1=45°,可得,|PF1|=2c,|PF2|=2$\sqrt{2}$c,结合椭圆的定义,即可求出C的离心率.
解答 解:由题意,|PF1|=2c,|PF2|=2$\sqrt{2}$c,
∴|PF1|+|PF2|=(2$\sqrt{2}$+2)c=2a,
∴e=$\frac{c}{a}$=$\frac{2}{2\sqrt{2}+2}$=$\sqrt{2}-1$,
故选:C.
点评 本题考查椭圆的定义域性质,考查学生的计算能力,比较基础.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
9.某人要制作一个三角形,要求它的三边的长度分别为3,4,6,则此人( )
| A. | 不能作出这样的三角形 | B. | 能作出一个锐角三角形 | ||
| C. | 能作出一个直角三角形 | D. | 能作出一个钝角三角形 |
19.已知F1,F2为双曲线C:x2-y2=2的左右焦点,点P在曲线C上,|PF1|=3|PF2|,则S${\;}_{△{F}_{1}{PF}_{2}}$=( )
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
3.函数f(x)=lg$\frac{1-x}{1+x}$在区间(-1,1)上是( )
| A. | 奇函数、增函数 | B. | 偶函数、增函数 | C. | 奇函数、减函数 | D. | 偶函数、减函数 |
4.下列各函数中,最小值为2的是( )
| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$ | C. | y=$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$ | D. | y=3x+3-x |
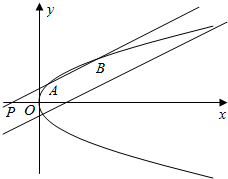 如图,已知抛物线C:y2=4x,点P(a,0),其中a<0,过点P作直线l1:x=my+a,与C交于不同的两点A,B
如图,已知抛物线C:y2=4x,点P(a,0),其中a<0,过点P作直线l1:x=my+a,与C交于不同的两点A,B