题目内容
【题目】如图所示，A ， B ， C是三个观察站，A在B的正东，两地相距6km，C在B的北偏西30°，两地相距4km，在某一时刻，A观察站发现某种信号，并知道该信号的传播速度为1km/s,4s后B ， C两个观察站同时发现这种信号，在以过A ， B两点的直线为x轴，以AB的垂直平分线为y轴建立的平面直角坐标系中，指出发出这种信号的P的坐标．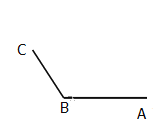
【答案】(8,5 
)
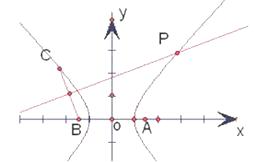
【解析】设点P的坐标为(x，y)，则A(3,0)，B(－3,0)，C(－5,2 )．
因为|PB|＝|PC|，所以点P在BC的中垂线上．
因为kBC＝－ ，BC的中点D(－4， )，
所以直线PD的方程为y－ ＝(x＋4)．①
又因为|PB|－|PA|＝4，所以点P必在以A，B为焦点的双曲线的右支上，
双曲线方程为－＝1(x≥2)．②
联立①②，解得x＝8或x＝－(舍去)，
所以y＝5
所以点P的坐标为(8,5 )．
练习册系列答案
相关题目
