题目内容
如图在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.
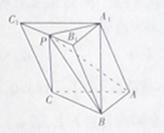
(1)证明:平面A1AC⊥平面AB1B;
(2)若点P为B1C1的中点,求三棱锥P-ABC与四棱锥P-AA1B1B的体积之比.

(1)证明:平面A1AC⊥平面AB1B;
(2)若点P为B1C1的中点,求三棱锥P-ABC与四棱锥P-AA1B1B的体积之比.
(1)证明详见解析;(2)1:1.
试题分析:(1)根据直线与平面垂直的性质可得
 ,而已知
,而已知 ,由直线与平面垂直的判定定理可得
,由直线与平面垂直的判定定理可得 面
面 ,根据平面与平面垂直的判定定理可得平面
,根据平面与平面垂直的判定定理可得平面 平面
平面 ;
;(2)由已知可知,
 =2是三棱锥P ABC的高,△ABC是等腰直角三角形,可计算出求三棱锥P ABC的体积.由于AC⊥平面AB1B,点P为B1C1的中点,可知点P到平面
=2是三棱锥P ABC的高,△ABC是等腰直角三角形,可计算出求三棱锥P ABC的体积.由于AC⊥平面AB1B,点P为B1C1的中点,可知点P到平面 距离
距离 等于点
等于点 到平面
到平面 的距离的一半,计算出四棱锥P AA1B1B的体积即可求解.
的距离的一半,计算出四棱锥P AA1B1B的体积即可求解.试题解析:证明:(1)由题意得:
 平面ABC,
平面ABC,∴
 , 2分
, 2分又
 ,
,
∴AC垂直平面AB1B, 3分
∵
 面
面 ,∴平面
,∴平面 平面
平面 ; 5分
; 5分(2)在三棱锥
 中,因为
中,因为 ,
,底面
 是等腰直角三角形,
是等腰直角三角形,
又因为点P到底面的距离
 =2,所以
=2,所以 . 6分
. 6分由(1)可知AC⊥平面AB1B,
因为点P在B1C1的中点,
所以点P到平面AA1B1B距离h2等于点C1到平面AA1B1B的距离的一半,即h2=1. 8分
 , 10分
, 10分所以三棱锥P ABC与四棱锥P AA1B1A1的体积之比为1:1. 12分

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
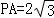 ,BC=CD=2,
,BC=CD=2,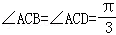 .
.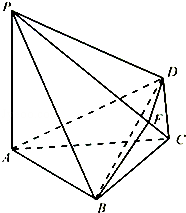
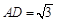 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.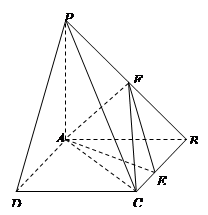
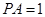 ,求证:
,求证: ;
;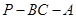 的大小为
的大小为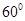 ,则CE为何值时,三棱锥
,则CE为何值时,三棱锥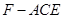 的体积为
的体积为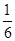 .
.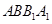 是圆柱体的轴截面,
是圆柱体的轴截面, 分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为
分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为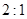 ,且该圆柱体的体积为
,且该圆柱体的体积为 ,如图所示.
,如图所示.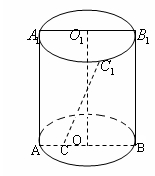
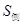 的值;
的值;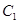 是半圆弧
是半圆弧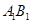 的中点,点
的中点,点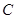 在半径
在半径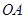 上,且
上,且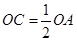 ,异面直线
,异面直线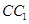 与
与 所成的角为
所成的角为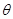 ,求
,求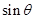 的值.
的值.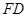 垂直于矩形
垂直于矩形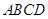 所在平面,
所在平面,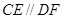 ,
,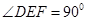 .
.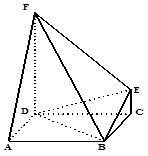
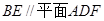 ;
;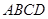 的一个边
的一个边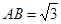 ,
,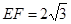 ,则另一边
,则另一边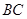 的长为何值时,三棱锥
的长为何值时,三棱锥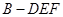 的体积为
的体积为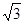 ?
? 中, 四边形
中, 四边形 为矩形,
为矩形,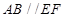 ,
, ,平面
,平面 平面
平面 、
、 分别为
分别为 、
、 的中点,且
的中点,且 ,
, .
.
 平面
平面 ;
; 平面
平面 ;
;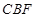 将几何体
将几何体 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为 ,
, ,求
,求 的值.
的值.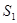 、
、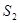 ,则
,则 ,高为2,则直三棱柱的外接球的表面积为( )
,高为2,则直三棱柱的外接球的表面积为( )



 中,
中, ,
, ,
, ,二面角
,二面角 的余弦值是
的余弦值是 ,若
,若 都在同一球面上,则该球的表面积是.
都在同一球面上,则该球的表面积是.